SHAP(SHapley Additive exPlanations)で機械学習モデルを解釈する
はじめに
ブラックボックスモデルを解釈する手法として、協力ゲーム理論のShapley Valueを応用したSHAP(SHapley Additive exPlanations)が非常に注目されています。SHAPは各インスタンスの予測値の解釈に使えるだけでなく、Partial Dependence Plotのように予測値と変数の関係をみることができ、さらに変数重要度としても解釈が可能であるなど、ミクロ的な解釈からマクロ的な解釈までを一貫して行える点で非常に優れた解釈手法です。
SHAPの論文の作者によって使いやすいPythonパッケージが開発されていることもあり、実際にパッケージを使った実用例はたくさん見かけるので、本記事では協力ゲーム理論の具体例、Shapley Valueのコンセプトと求め方、機械学習モデルを解釈するためのShapley Valueの使われ方を意識してまとめました。
※この記事をベースに2020年1月16日に行われたData Gateway Talk vol.5にて発表した資料は以下になります
speakerdeck.com
※この記事で紹介するSHAPを含んだ、機械学習の解釈手法に関する本を書きました!
この記事で書いていること、書いていないこと
書いていること
書いていないこと
アルバイトゲームとShapley Value
ここでは協力ゲーム理論のアルバイトゲームを例にとって、Shapley Valueを直感的に理解することを目指します。
まずはアルバイトゲームについて説明します。*1
アルバイトは単独で行うこともできますし、他の人とチームを組んでやってもいいとします。
- まずは、1人で働いた場合は、A君が1人でやると6万円、B君が1人でやると4万円、C君が1人でやると2万円がもらえるとしましょう。
- 次に、2人で働いた場合は、A君とB君が2人でやったときは合計で20万円、A君とC君が2人でやったときは合計で15万円、B君とC君が2人でやったときは合計で10万円がもらえるとしましょう。
- 最後に、A君B君C君の3人で働いた場合は、合計で24万円がもらえるとしましょう。
これをまとめると以下の表のようになります。
| 参加者 | 報酬 |
|---|---|
| A君 | 6 |
| B君 | 4 |
| C君 | 2 |
| A君B君 | 20 |
| A君C君 | 15 |
| B君C君 | 10 |
| A君B君C君 | 24 |
今、A君B君C君の3人全員で働いて得た報酬24万円をどうやって分配するのが尤もらしいかを考えます。
直感的には、より貢献度の高い人による多くの報酬を分配するのがフェアな分配のひとつになりそうです。*2
とすると、問題は各人の貢献度をどうやって計るのかということになります。ここで限界貢献度という概念を導入しましょう。これは「各人がアルバイトに参加したときに追加的にどのくらい報酬が増えるか」で計算されます。
たとえば、A君について考えると、限界貢献度は以下のように計算されます。
- 「誰もいない」→「A君のみ」だと6 - 0 = 6万円
- 「B君のみ」→「A君とB君」だと20 - 4 = 16万円
- 「C君のみ」→「A君とC君」だと15 - 2 = 13万円
- 「B君とC君」→「A君とB君とC君」だと24 - 10 = 14万円
ここでわかるのは、A君の限界報酬はA君が参加する順番に依存するということです。
この影響を打ち消すため、考えられる全ての参加順を用いて平均的な限界貢献度を求めることにしましょう。
発生し得る参加順と、その場合の各人の限界貢献度は以下のようにまとめられます。
| 参加順 | A君の限界貢献度 | B君の限界貢献度 | C君の限界貢献度 |
|---|---|---|---|
| A君→B君→C君 | 6 | 14 | 4 |
| A君→C君→B君 | 6 | 9 | 9 |
| B君→A君→C君 | 16 | 4 | 4 |
| B君→C君→A君 | 14 | 4 | 6 |
| C君→A君→B君 | 13 | 9 | 2 |
| C君→B君→A君 | 14 | 8 | 2 |
参加順は3!=6通りなので、
- A君の平均的な限界貢献度は(6 + 6 + 16 + 14 + 13 + 14) / 6 = 11.5万円
- B君の平均的な限界貢献度は(14 + 9 + 4 + 4 + 9 + 8) / 6 = 8万円
- C君の平均的な限界貢献度は(4 + 9 + 4 + 6 + 2 + 2) / 6 = 4.5万円
この平均的な限界貢献度のことをShapley Valueと言い、このShapley Valueを用いて報酬を分配しよう、というのがある意味で尤もらしい分配の方法になります。実際、11.5 + 8 + 4.5 = 24万円できれいに分配ができていますし、より貢献度が高い人により多くの報酬が渡るという意味でフェアな分配にもなっています。*3
今回はゲームのプレイヤーがA君B君C君3人のケースを考えました。より一般的なケースとして人のプレイヤー
がゲームに参加するケースを考えると、プレイヤー
のShapley Value
は以下で計算できます。
\begin{align*}
\phi_i =
\sum_{\mathcal{S} \subset\mathcal{N} \setminus \{i\}}
\frac{S!(N - S - 1)!}{N!}
\bigg(v(\mathcal{S}\cup \{i\}) - v(\mathcal{S})\bigg)
\end{align*}
- ここで、
は
からプレイヤー
を除いたプレイヤーの組み合わせです。たとえばA君B君C君3人のケースで、A君のShapley Valueを考える場合は、
が該当します。
は
の要素の数、つまりプレイヤーの数になります。先程の例だと、それぞれ0人, 1人, 1人, 2人となります。
は効用を表す関数です。なので、
はプレイヤー
が参加しているときと参加していないときでの効用の差となります。つまり、プレイヤー
が参加したときの限界貢献度となります。
まとめると、プレイヤーが参加することの限界貢献度を出現する全ての組合わせで求めて平均しています。これはアルバイトゲームの具体例でやったことと全く同じ操作をしています。上式だけみると何を計算しているかよくわからないのですが、具体例をいれて確かめてみると何をやっているかわかりやすいんじゃないかと思います。
機械学習モデルへの応用
最近、協力ゲーム理論のShapley Valueを機械学習モデルの予測結果を解釈するために利用しよう、という研究が発達してきました。
これらの研究では、モデルに投入したひとつひとつの特徴量をゲームのプレイヤーと見立てて、各特徴量の予測への貢献度をShapley Valueで測ろう、ということをやっています。
具体的なシチュエーションを考えてみましょう。今、特徴量としての3つがあるとします。
モデルをとすると、平均的な予測値は
]となります。
ここで、ひとつのインスタンスを取り出すと、それぞれ という値をとっているとします。このとき、予測値としては
が出力されます。
この、平均的な予測値]と各インスタンスの予測値
の乖離に対して、各特徴量がどのくらい影響しているのかを調べます。
各インスタンスの予測値は
\begin{align*}
E[f( \mathbf{X} | X_1 = x_1, X_2 = x_2, X_3 = x_3)] & = f( x_1, x_2, x_3 ) = f(\mathbf{x})
\end{align*}
なので、平均的な予測値]から
を条件付けていくことで、その特徴量を知ることが各インスタンスの予測に対してどのように影響するかを知ることができます。具体的に、
の順で条件づけていくとすると、たとえば下図のような推移が見られます。

ここで、を各特徴量が予測値に与える限界的な効果としています。(なお、
は0と平均的な予測値の乖離で、特に重要ではありません。)
まず、特に何の情報もないところからという情報を得ると、予測値が
だけ大きくなります。さらにその状態から
という情報を得ると、予測値がさらに
だけ大きくなります。最後に、
という情報を得ると、予測値が
だけ小さくなって、これが最終的なこのインスタンスへの予測結果となります。
ここで、先程のアルバイトゲームとの共通点が現れています。
- 各特徴量を一つずつ条件付けていくことで予測値に与える限界的な効果を見ていますが、これはアルバイトゲームで言うところの限界貢献度に対応しています。
- また、今回は
の順で条件づけていますが、当然別の順番で条件づけていくと予測値に与える限界的な効果は変化します。よって、考えうる全ての順序で限界効果を計算し、それを平均しなければなりません。この平均的な限界効果がShapley Valueに対応します。
詳細は論文をご確認頂きたいのですが、このようにShapley Valueを用いて計算された貢献度は、Shapley Valueが持つ望ましい性質を満たすことが証明されています。
ただ、Shapley Valueを計算するのは非常に計算コストがかかるので、実際の計算ではアルゴリズムごとの近似手法が用いられています。特に、tree系のアルゴリズムに対してはTreeSAHPという高速なアルゴリズムが提案されています。
機械学習モデルに対するShapley Valueを簡単で高速に計算できるPythonパッケージにSHAPがあります。
まずは必要なパッケージを読み込みましょう。
import numpy as np import pandas as pd # モデルはRandom Forestを使う from sklearn.ensemble import RandomForestRegressor # SHAP(SHapley Additive exPlanations) import shap shap.initjs() # いくつかの可視化で必要
データはshapパッケージにあるボストンの不動産価格のデータを用います。
データセットの細かい説明はリンクをご確認下さい。
X, y = shap.datasets.boston() X.head()

モデルはRandom Forestを使います。
model = RandomForestRegressor(n_estimators=500, n_jobs=-1) model.fit(X, y)
ここからがshapの使い方になります。shapにはいくつかのExplainerが用意されていて、まずはExplainerにモデルを渡すします。今回はRandom ForestなのでTreeExplainer()を使います。
explainer = shap.TreeExplainer(model, X)
Explainerにはshap_values()メソッドが用意されています。これにShapley Valueを計算したいインプットの行列を渡すことでShapley Valueを計算できます。shapは高速な計算アルゴリズムが実装されており、特にこのデータセットは500行程度なのですぐに計算は終わりますが、計算コストは依然として高いので大きいデータセットのときは適当にサンプリングして渡す必要があります。
shap_values = explainer.shap_values(X)
まずは一つのインスタンスに対してShapley Valueを確認してみます。これは`force_plot()`を使います。
i = 0
shap.force_plot(explainer.expected_value, shap_values[i,:], X.iloc[i,:])

basevalueの22.51がが全体平均で、output valueの25.64がこのインスタンスに対する予測値となります。なので、このインスタンスは平均よりも高い値が予測されています。なぜこのような予測になったのかを説明するために、各特徴量がどのくらい大きな因子となっているのかを、Shapley Valueで分解して可視化しています。たとえば、このインスタンスはLSTATが4.98をとっていて、これはこのインスタンスの不動産価格に対して大きなプラスの要因となっています。逆に、RMは6.575となっていて、これはマイナス要因であることも見て取れます。プラスとマイナスを総合するとプラスの方が大きくなっていて、最終的には全体平均より3.13高い予測結果になっていることがわかります。
ちなみにLSTATはその地域に住む低所得層の割合、RMは平均的な部屋の数です。
ひとつひとつのインスタンスでShapley Valueを見ていくことでミクロな分析ができますが、よりマクロな分析として、Shapley Valueを変数ごとに平均して変数重要度のように使うこともできます。
今、データセットのインスタンス数がとすると、変数
の変数重要度
は以下で計算します。
\begin{align*}
\mathrm{Feature Importance}_p = \frac{1}{N}\sum_{i = 1}^{N} \left|\phi_p^i \right|
\end{align*}
ただし、はインスタンス
での変数
のShapley Valueです。また、プラスマイナスの影響を無視するために絶対値をとっています。
この変数重要度を簡単に可視化するための関数として、summry_plot()が用意されています。
shap.summary_plot(shap_values, X, plot_type="bar")

Shapley Valueの意味で、LSTATとRMが非常に重要な変数であることが見て取れます。
plot_type = "bar"とすると棒グラフが出ますが、指定しないと一つ一つのShapley Valueがそのまま打たれます。*4
shap.summary_plot(shap_values, X)
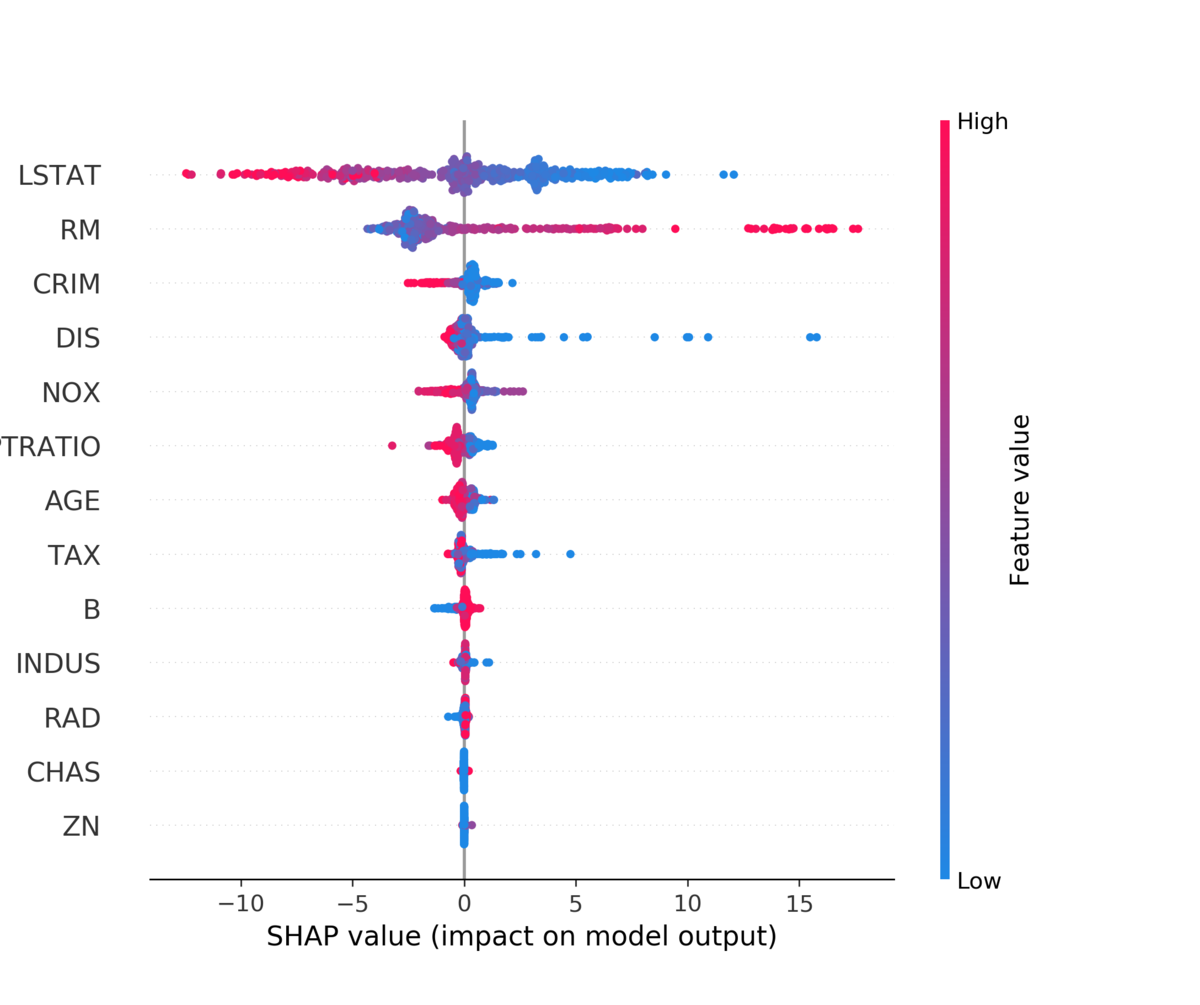
上に来るほど先程の棒グラフの意味で重要な変数になります。色が赤いほどその変数の値が高いとき、青いほど低いときのShapley Valueになります。Shapley Valueの分布に加えて、LSTATは低いほうがプラスの要因に、RMは高いほうがプラスの要因になりそうなことが見て取れます。
さらに、特徴量の値とShapley Valueの散布図を書くことで、Partial Dependence Plotのような可視化も可能となります。
これは dependence_plot()を使います。今回は特に重要度の高かったLSTATを見てみましょう。
shap.dependence_plot("LSTAT", shap_values, X)

LSTATの値が大きくなるほどShapley Valueが小さくなることが見て取れます。
色付けは交互作用が見れるように他の変数の値でされています。デフォルトでは交互作用が一番はっきり現れる変数が自動で選ばれます。今回はDISが選ばれていて、DISの値が大きいほど赤く、小さいほど青い点が打たれます。DISはemployment centreからの距離を表しています。グラフの左半分を見ると、同じLSTATの値でもDISが短いほどShapley Valueが高くなる傾向が見て取れます。
参考文献
- 岡田卓『ゲーム理論 新版』
- A Unified Approach to Interpreting Model Predictions
- [1802.03888] Consistent Individualized Feature Attribution for Tree Ensembles
- GitHub - slundberg/shap: A game theoretic approach to explain the output of any machine learning model.
- 5.9 Shapley Values | Interpretable Machine Learning
- 5.10 SHAP (SHapley Additive exPlanations) | Interpretable Machine Learning
- https://pbiecek.github.io/PM_VEE/shapley.html
- 可視化アルゴリズムSHAPを理解するために、ゲーム理論を調べてまとめました。 - データ分析関連のまとめ
*1:この数値例は岡田章『新板ゲーム理論』の例をそのままお借りしています。
*2:たとえば、山分けで3等分も考えられますが、この設定ではそれはうまくいきません。A君B君C君の3人で働いて3等分すると報酬は8万円になります。この場合、A君B君だけで働いて報酬を2等分するとA君とB君は10万円を稼ぐことができ、C君を外すインセンティブが生まれてしまいます。
*3:Shapley Valueは数学的に証明された望ましい性質をいくつかもっていますが、ここでは具体例と直感的な性質のみ説明しています。詳細を知りたい場合は協力ゲーム理論の教科書か論文をご確認下さい。
*4:僕はこれの正式な名称を知りません。sina plotでいいのかな?
