多重共線性と回帰係数の信頼性の話。あとリッジ回帰。

$\def\paren#1{\left(#1\right)} \def\brac#1{\left[#1\right]} \def\sumi{\sum_{i=1}^N} \def\P#1{\Pr\paren{#1}} \def\E#1{\mathbb{E}\brac{#1}} \def\var#1{\mathrm{Var}\brac{#1}} \def\hvar#1{\widehat{\mathrm{Var}}\brac{#1}} \def\quad#1{\paren{#1}^2} \def\inv#1{\paren{#1}^{-1}} \def\Xij{X_{i, j}} \def\vX{\mathbf{X}} \def\vXj{\mathbf{X}_j} \def\vXmj{\mathbf{X}_{\setminus j}} \def\vY{\mathbf{Y}} \def\vU{\mathbf{U}} \def\hvU{\hat{\vU}} \def\vVj{\mathbf{V}_j} \def\hvVj{\hat{\mathbf{V}}_j} \def\mM{\mathbf{M}} \def\mMj{\mathbf{M}_j} \def\mMmj{\mathbf{M}_{\setminus j}} \def\vP{\mathbf{P}} \def\mW{\mathbf{W}} \def\vI{\mathbf{I}} \def\hbeta{\hat{\beta}} \def\betamj{\beta_{\setminus j}} \def\hbetamj{\hbeta_{\setminus j}} \def\hgamma{\hat{\gamma}} \def\hXij{\hat{X}_{i, j}} \def\hVij{\hat{V}_{i, j}} \def\bXj{\bar{X}_{j}}$

はじめに
多重共線性とOLS推定量の信頼度
シミュレーションによる信頼度の確認
リッジ推定量で推定量の信頼性を高める
まとめ
参考文献

はじめに

先日、多重共線性に関する @hizakayuさんや@M123Takahashiさんのコメントを目にしました。

多重共線性の問題は，どの説明変数に強い相関があるかにより変わります．たとえば，y=b0+b1x1+b2x2+b3x3で，x1からyへの効果b1に興味があり，x2とx3は交絡因子とします．cor(x1,x2)>0.9は問題になり得ますが，cor(x2,x3)>0.9は気にする必要はありません．b2とb3の推定には興味がないからです．（続く） https://t.co/4d0gDukAB4
— 高橋将宜 Masayoshi Takahashi (@M123Takahashi) 2021年6月14日

【多重共線性と推定値の話】
昨日、これについて、教科書を紹介してもらい、勉強して少しまとめたので、Twitterの海に流します🌊 https://t.co/kDbySASiuj
— コムラ (@hizakayu) 2021年6月15日

恥ずかしながら、ここで紹介されている多重共線性と推定量の信頼性に関する性質のことは普通に忘れていました。
こちらのコメントを見てそういえばこんなこと習ったなと思い出し、大学院のころの資料*1や計量経済学の教科書*2を確認し、改めて学びなおしたことを記事としてまとめました。

この記事では、まずは多重共線性がある場合のOLS推定量の分散について数式を用いて確認します。
次に、数式で確認した結果をシミュレーションを用いて実際にみていきます。
最後に、推定量の信頼性を高める手法としてリッジ推定量を紹介し、リッジ推定量は（バイアスという犠牲を払うことで）信頼性を高められるを確認します。

多重共線性とOLS推定量の信頼度

線形回帰モデルの導入

以下のような線形回帰モデル

\begin{align}
Y_i = X_i'\beta + U_i
\end{align}

を考えます。ここで、 $Y_i$ は目的変数、 $X_i = (X_{i, 1}, \dots, X_{i, J})'$ は説明変数、 $U_i$ は誤差項を表します。
$i = 1, \dots, N$ はサンプルを表す添字で、 $\{X_i, Y_i\}_{i=1}^N$ はランダムサンプリングされているとします。
$\beta = (\beta_1, \dots, \beta_J)'$ は回帰係数です。

以下、表記を単純にするため行列を利用します。

\begin{align}
\vY = \vX\beta + \vU
\end{align}

それぞれの行列は以下で構成されています。

\begin{align}
\vY = \underbrace{\begin{pmatrix}
Y_1 \\
\vdots \\
Y_N
\end{pmatrix}}_{N \times 1},\;\;
\vX = \begin{pmatrix}
X_{1}'\\
\vdots \\
X_{N}'
\end{pmatrix}
= \underbrace{\begin{pmatrix}
X_{1, 1} & \cdots & X_{1, J}\\
\vdots & \ddots & \vdots \\
X_{N, 1} & \cdots & X_{N, J}
\end{pmatrix}}_{N \times J},\;\;
\vU = \underbrace{\begin{pmatrix}
U_1 \\
\vdots \\
U_N
\end{pmatrix}}_{N \times 1}
\end{align}

標準的な仮定として $\E{\vU \mid \vX} = 0$ をおきます。
また、話を簡単にするために、分散均一性 $\var{\vU \mid \vX} = \sigma^2\vI_N$ も仮定しておきます。

OLS推定量

このとき、最小二乗法（Ordinary Least Squares）を用いた推定量は以下で与えられます。

\begin{align}
\hbeta &= \arg\min_{\beta} \paren{\vY - \vX\beta}'\paren{\vY - \vX\beta}\\
&=\inv{\vX'\vX}\vX'\vY
\end{align}

これをOLS推定量と呼びます。
いま興味があるのは、このOLS推定量の信頼度と多重共線性の関係です。
この記事では、多重共線性があるとOLSを推定量の信頼性が低くなっていくことを示します。

まず第一に、もし完全な多重共線性が発生していると、 $\vX'\vX$ がランク落ちして逆行列が取れません。
よって、完全な多重共線性がある場合はそもそも回帰係数が推定できないということになります。
これは多重共線性が最も問題になるケースです。
この場合、完全な多重共線性を回避すべく余計な説明変数を削除するなどの調整が必要になります。

以下では、完全な多重共線性は起きていないとして話を進めます。
つまり、 $\vX'\vX$ がフルランクであることを仮定します。
$\vY = \vX\beta + \vU$ だったことを思い出すと、OLS推定量 $\hbeta$ は以下のように変形できます。

\begin{align}
\hbeta &= \inv{\vX'\vX}\vX'\paren{\vX\beta + \vU}\\
&= \inv{\vX'\vX}\vX'\vX\beta + \inv{\vX'\vX}\vX'\vU\\
&= \beta + \inv{\vX'\vX}\vX'\vU
\end{align}

この変形からOLSを推定量に関する重要な指標である期待値と分散を知ることができます。
まずは期待値をとると、 $\E{\vU \mid \vX} = 0$ の仮定のおかげで

\begin{align}
\E{\hbeta \mid \vX} &= \beta + \inv{\vX'\vX}\vX'\E{\vU \mid \vX}\\
&= \beta
\end{align}

となり、OLS推定量の期待値は真の回帰係数 $\beta$ と一致することがわかります。
この性質は不偏性と呼ばれています。

また、OLS推定量の分散は

$\begin{align} \var{\hbeta_j \mid \vX} &= \var{\inv{\vX'\vX}\vX'\vU \mid \vX}\\ &= \inv{\vX'\vX}\vX'\var{\vU \mid \vX}\vX\inv{\vX'\vX}\\ &= \inv{\vX'\vX}\vX'\sigma^2\vI_N\vX\inv{\vX'\vX}\\ &= \inv{\vX'\vX}\sigma^2 \end{align}$

となることがわかります。
ここで、分散均一性の仮定 $\var{\vU \mid \vX} = \sigma^2\vI_N$ を使っていることに注意して下さい。

推定量の分散はその推定量がどのくらい安定しているのかを表す指標と言えます。
実際、推定量の分散の平方根をとったものは標準誤差と呼ばれていて、信頼区間の計算や統計的仮説検定に利用します。

ところで、いま知りたいことは、多重共線性と推定量の信頼度（＝分散）の関係でした。
残念ながら、 $\var{\hbeta_j \mid \vX} = \inv{\vX'\vX}\sigma^2$ という式からは多重共線性がある場合に分散がどうなるのかいまいち想像ができません。
そこで、 $\var{\hbeta_j \mid \vX}$ を別の形で表現することにします。

Annihilator Matrix

後の行列操作を楽にするために、Annihilator Matrix $\mM$ を導入します（これがなぜAnnihilatorと呼ばれているのかはよくわかりません）。

\begin{align}
\mM = \vI_N - \vX\inv{\vX'\vX}\vX'
\end{align}

行列 $\mM$ は以下の性質を持ちます。
かなり便利なのでこの記事を読む間だけ覚えておいてください。

$\mM' = \mM$ ：転地しても同じ行列
$\mM\mM = \mM$ ：かけても同じ行列
$\mM\vX = 0$ ：説明変数にかけるとゼロ
$\mM\vY = \vY - \vX\hbeta = \hvU$ ：目的変数にかけると残差になる

実際、簡単な行列計算から上記の性質が成り立っていることが見て取れます。

\begin{align}
\mM'
&= \paren{ \vI_N - \vX\inv{\vX'\vX}\vX'}' \\
&= \vI_N - \vX\inv{\vX'\vX}\vX' \\
&= \mM\\
\mM\mM
&= \paren{ \vI_N - \vX\inv{\vX'\vX}\vX'}\paren{\vI_N - \vX\inv{\vX'\vX}\vX'} \\
&= \vI_N - \vX\inv{\vX'\vX}\vX' - \vX\inv{\vX'\vX}\vX' + \vX\inv{\vX'\vX}\vX' \\
&= \mM\\
\mM\vX &= X - \vX\inv{\vX'\vX}\vX'\vX \\
&= 0\\
\mM\vY &= Y - \vX\inv{\vX'\vX}\vX'\vY \\
&= \vY - X\hbeta\\
&= \hvU
\end{align}

$\mM\vY = \vY - \vX\hbeta = \hvU$ という性質から、 $\mM$ は線形回帰モデルの残差を作る行列として知られています。

OLS推定量の別表現

それでは、残差を作る行列 $\mM$ を用いてOLS推定量を別の形で表現できることを示します。
まず、線形回帰モデルを説明変数 $\vXj$ に関する部分と、それ以外の部分 $\vXmj$ に分解します。

\begin{align}
\vY = \vXj\beta_j + \vXmj\betamj + \vU
\end{align}

ここで、それぞれの行列は以下を表しています。

\begin{align}
\vXj &= (X_{1, j}, \dots, X_{N, j})'\\
\vXmj &= (\vX_1, \dots, \vX_{j-1}, \vX_{j+1}, \dots \vX_{J})\\
\betamj &= (\beta_1, \dots, \beta_{j-1}, \beta_{j+1}, \dots \beta_{J})'
\end{align}

いま、説明変数 $\vXj$ に対するOLS推定量 $\hbeta_j$ を知りたいとします。
通常の最小二乗法はすべての $\beta$ を同時に動かして二乗誤差を最小にしますが、
まず $\betamj$ を動かして二乗誤差を最小にし、残った部分に対して改めて $\beta_j$ を動かして二乗誤差を最小にする $\hbeta_j$ を求める、という二段階のステップを踏んでも同じ結果になります。
この操作を数式で表現すると以下になります。

\begin{align}
\hbeta_j &= \arg\min_{\beta_j}\brac{\min_{\betamj}\paren{\vY - \vXj\beta_j - \vXmj\betamj}'\paren{\vY - \vXj\beta_j - \vXmj\betamj}}
\end{align}

内側の最小化問題をよく見ると、これは $\vY - \vXj\beta_j$ に対して $\vXmj\betamj$ で回帰していると解釈できるので、そのOLS推定量は以下で求めることができます。

\begin{align}
\hbetamj &= \inv{\vXmj'\vXmj}\vXmj'\paren{\vY - \vXj\beta_j}
\end{align}

これを内側の最小化問題に戻すことを考えると

\begin{align}
\vY - \vXj\beta_j - \vXmj\hbetamj
&= \vY - \vXj\beta_j - \vXmj\inv{\vXmj'\vXmj}\vXmj'\paren{\vY - \vXj\beta_j}\\
&= \paren{\vI_N - \vXmj\inv{\vXmj'\vXmj}\vXmj'}\paren{\vY - \vXj\beta_j}\\
& = \mMmj\paren{\vY - \vXj\beta_j}\\
&= \mMmj\vY - \mMmj\vXj\beta_j
\end{align}

なので、元の最小化問題は

\begin{align}
\hbeta_j &= \arg\min_{\beta_j}\paren{\mMmj\vY - \mMmj\vXj\beta_j}\paren{\mMmj\vY - \mMmj\vXj\beta_j}
\end{align}

となることが分かります。

ここから、OLS推定量は

\begin{align}
\hbeta_j &= \inv{\vXj'\mMmj'\mMmj\vXj}\vXj'\mMmj'\mMmj\vY\\
&= \inv{\vXj'\mMmj\vXj}\vXj'\mMmj\vY\\
\end{align}

という形式でも表現できることがわかりました。

補助回帰

OLS推定量を別形式で表現できましたが、ここに出てくる $\mMmj\vXj$ は何を計算しているのでしょうか？
残差を作る行列 $\mMmj$ の意味を考えると、 $\mMmj\vXj$ は説明変数 $\vXj$ を他の説明変数 $\vXmj$ で回帰したときの残差を表しています。
つまり、線形回帰モデル

\begin{align}
\vXj = \vXmj\gamma + \vVj
\end{align}

に対する残差

\begin{align}
\mMmj\vXj = \vXj - \vXmj\inv{\vXmj'\vXmj}\vXmj'\vXj = \vXj - \vXmj\hgamma = \hvVj
\end{align}

を表現しています。
説明変数 $\vXj$ をその他の説明変数 $\vXmj$ で回帰することは補助回帰（auxiliary regression）と呼ばれています。
残差が $\hvVj$ 小さければ、説明変数 $\vXj$ は他の説明変数 $\vXmj$ でほぼ表現できてしまうということになります。
この場合、説明変数 $\vXj$ は追加的に与える情報量の少ない説明変数ということになります。
一方で、残差が $\hvVj$ が大きい場合は、説明変数 $\vXj$ は他の説明変数では与えることのできない情報をモデルに与えていると言えます。

これを多重共線性の文脈でいうと、残差 $\hvVj$ が小さいことは（説明変数 $\vXj$ に対する）多重共線性が強いことに対応し、残差 $\hvVj$ が大きいことは多重共線性が弱いことに対応します。
実際、完全な多重共線性がある状態として $\vXj = \vX_k$ となるような別の特徴量が存在するケースを考えると、残差 $\hvVj$ もゼロになります。

OLS推定量の分散を解釈する

それでは、改めてOLS推定量の分散について考えましょう。
$\vY = vXj\beta_j + \vXmj\betamj + \vU$ であったことを思い出すと、OLS推定量は以下のように変形できます。

\begin{align}
\hbeta_j &= \inv{\vXj'\mMmj \vXj}\vXj'\mMmj\paren{\vXj\beta_j + \vXmj\betamj + \vU}\\
&= \underbrace{\inv{\vXj'\mMmj \vXj}\vXj'\mMmj\vXj}_{=\vI_J}\beta_j
+ \inv{\vXj'\mMmj \vXj}\vXj'\underbrace{\mMmj\vXmj}_{=0}\betamj
+ \inv{\vXj'\mMmj \vXj}\vXj'\mMmj\vU\\
&= \beta_j + \inv{\vXj'\mMmj \vXj}\vXj'\mMmj\vU\\
&= \beta_j + \inv{\vXj'\mMmj\mMmj\vXj}\vXj'\mMmj\mMmj\vU\\
&= \beta_j + \inv{\hvVj'\hvVj}\hvVj'\vU
\end{align}

これの分散をとると

$\begin{align} \var{\hbeta_j \mid \vX} &= \var{\inv{\hvVj'\hvVj}\hvVj'\vU \mid \vX}\\ &= \inv{\hvVj'\hvVj}\hvVj'\var{\vU \mid \vX}\hvVj\inv{\hvVj'\hvVj}\\ &= \inv{\hvVj'\hvVj}\hvVj'\sigma^2\vI_N\hvVj\inv{\hvVj'\hvVj}\\ &= \inv{\hvVj'\hvVj}\sigma^2 \end{align}$

となります。
さらに、 $\hvVj'\hvVj = \sumi \hVij^2 = \sumi\quad{\Xij - \hXij}$ であることを利用すると、

$\begin{align} \var{\hbeta_j \mid \vX} &= \frac{\sigma^2}{\sumi\quad{\Xij - \hXij}} \end{align}$

と表現できます。
説明変数 $\vXj$ の平均を $\bXj = \frac{1}{N}\sumi X_{i, j}$ として、分母に $\sumi \quad{\Xij - \bXj}$ をかけて割ると

$\begin{align} \var{\hbeta_j \mid \vX} &= \frac{\sigma^2}{\sumi \quad{\Xij - \hXij} / \sumi \quad{\Xij - \bXj}} \times \frac{1}{N \times \frac{1}{N}\sumi \quad{\Xij - \bXj}}\\ &= \frac{\sigma^2}{N\paren{1 - R^2_j}\hvar{X_j}} \end{align}$

を得ます。
ここで、
\begin{align}
R^2_j = 1 - \frac{\sumi \quad{\Xij - \hXij}}{\sumi \quad{\Xij - \bXj}}
\end{align}
は説明変数 $\vXj$ をその他の説明変数 $\vXmj$ で回帰したときの決定係数です。 $\vXj$ のばらつきのうち平均では説明できなかった部分を $\vXmj$ でどのくらい説明できるかを表しています。つまり、多重共線性の強さを表す指標です。ちなみに、 $\vXmj$ が一変数の場合は相関係数の二乗に相当します。

また、 $\hvar{X_j}$ は説明変数 $\vX_j$ の標本分散を表しています。

さて、ここまで長い道のりでしたが、この表現から多重共線性がOLS推定量の分散（信頼度）にどう影響するかを解釈することができます。

1. 説明変数 $\vX$ では説明できない目的変数 $\vY$ の変動 $\sigma^2$ が大きければ大きいほど、分散が大きくなる
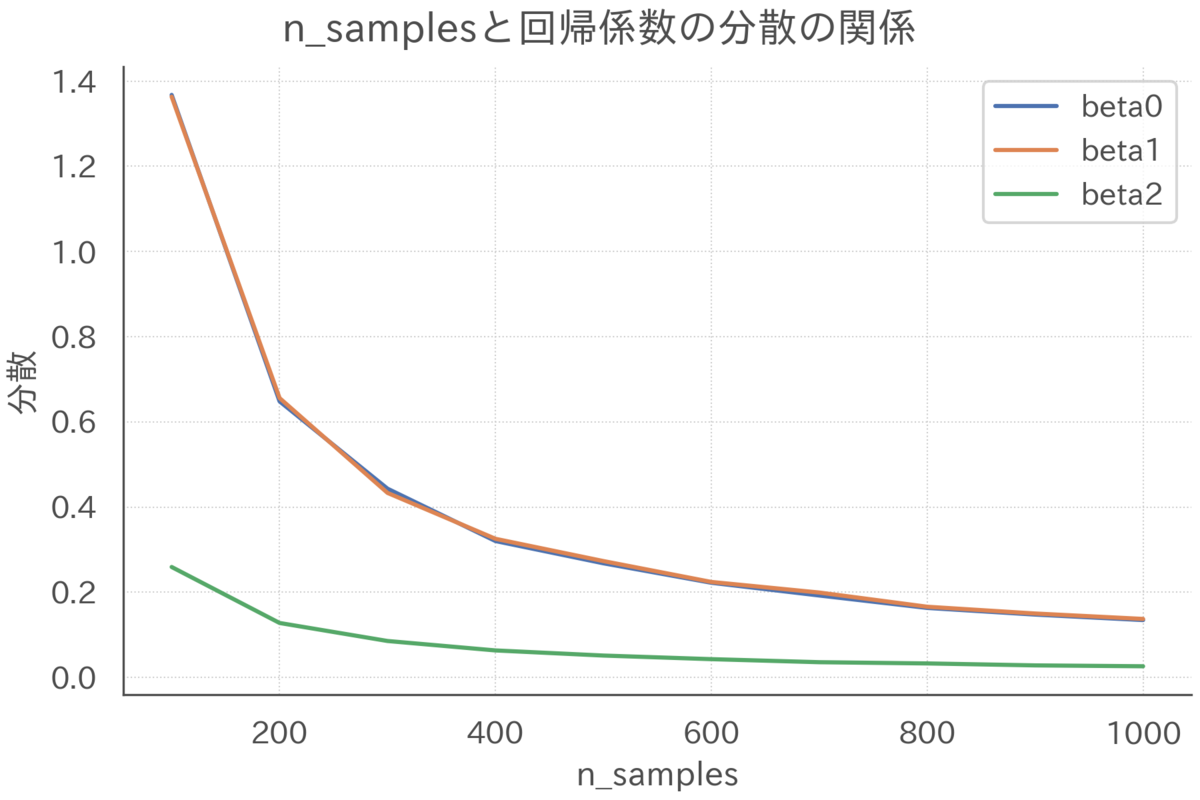
2. サンプルサイズ $N$ が大きくなると、分散が小さくなる
3. 説明変数 $\vX_j$ の標本分散 $\hvar{X_j}$ が大きくなると、分散が小さくなる
4. 決定係数 $R^2_j$ が大きくなると、分散が大きくなる

1.はデータの限界みたいなところがあるので言っても仕方ないかなと思っています。

2.は当たり前といえば当たり前で、データが多いと推定量の信頼性が上がっていくのはよく言われていることですね。
ただ、 $\var{\hbeta_j \mid \vX} = \inv{\vX'\vX}\sigma^2$ という表現からは明示的には見えてこなかった部分ではあります。

3.は説明変数の取りうる値のレンジが大きいと回帰係数が小さくなることからくる性質なので、これもあんまり気にしなくていいと思います。
実際、説明変数をあらかじめ標準化すると分散が1になるので無視できます。
これも $\var{\hbeta_j \mid \vX} = \inv{\vX'\vX}\sigma^2$ という表現からは明示的には見えてこなかった部分ではあります。

やはり重要なのは4.で、説明変数 $\vXj$ をその他の説明変数 $\vXmj$ で説明できてしまう割合が大きいと、OLS推定量 $\hbeta_j$ の信頼性が下がることが見て取れます。
つまり、多重共線性があるケースで推定量の信頼性が下がることがわかります。
ここで重要なことは、 $\hbeta_j$ の信頼性に影響するのはあくまで $\hbeta_j$ に対する決定係数 $R_j^2$ であることです。
言い換えると、 $\vXj$ とは関係ない説明変数同士で強い相関があったとしても、それらの説明変数が $\vXj$ に対して説明力を持たないのであれば、 $\hbeta_j$ の信頼性に特に影響は与えません。
ですので、多重共線性を考える際には、あくまでいま興味のあるターゲットの説明変数 $\vXj$ に対する多重共線性のみに注意すればよく、他の説明変数で多重共線性が起きていても（その説明変数の回帰係数に興味がないなら）無視しても良いと言えます。

これが特に重要になってくるのは因果関係を考えるケースで、多重共線性を気にしてコントロール変数をむやみにモデルから外すと欠落変数バイアスが発生してしまいます。
ターゲットの説明変数と無関係の多重共線性は気にせず、論理的に入れるべきコントロール変数は入れるべきだと思います。
ターゲットの説明変数に対して強い多重共線性が発生しているケースは問題といえば問題だとは思うのですが、そもそもコントロール変数でほとんどの部分が説明できてしまう変数をターゲットにするのはどうなんだという話にもなるかなと思っています。

まとめると、完全な多重共線性はそもそも計算ができないので問題ですが、そうでなければ多重共線性はあまり気にしなくていいケースがほとんどだと思っています。

シミュレーションによる信頼度の確認

シミュレーションの設定

OLS推定量の分散の振る舞いを数式からも確認しましたが、ここではシミュレーションを用いて理解を深めることにします。
以下の設定でシミュレーションデータを生成します。

$\begin{align} Y &= X_0 + X_1 + X_2 + U\\ (X_0, X_1, X_2) &\sim \mathcal{N}\paren{ \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix},\; \begin{pmatrix} 1 & \rho & 0\\ \rho & 1 & 0\\ 0 & 0 & 1 \end{pmatrix} }\\ U &\sim \mathcal{N}\paren{0, \sigma^2} \end{align}$

ここで、説明変数 $X_0$ と $X_1$ は相関していて、 $X_2$ は無相関であるような設定を考えています。
話を単純にするために、回帰係数 $(\beta_0, \beta_1, \beta_1)$ はすべて1としています。

多重共線性とOLS推定量の信頼度

まずは多重共線性がOLS推定量の分散に与える影響を見ていきます。
多重共線性の強さによる影響の大きさを知るために、説明変数 $X_0$ と $X_1$ の相関係数 $\rho$ を変化させた場合の分散の大きさを確認します。

f:id:dropout009:20210722194753p:plain

上図を確認すると、説明変数 $(X_0, X_1)$ の相関が強くなるにつれて、 $(\beta_0, \beta_1)$ に関するOLS推定量の分散 $\hvar{\beta_0 \mid \vX}$ と $\hvar{\beta_1 \mid \vX}$ が大きくなっていく様子が見て取れます。
よって、多重共線性が強くなると推定量の信頼性は低くなると言えます。

一方で、説明変数 $(X_0, X_1)$ の相関は、 $\beta_2$ に関するOLS推定量の分散 $\hvar{\beta_2 \mid \vX}$ にはなんの影響も与えていないこともわかります。
数式でも確認したように、もし回帰係数 $\beta_2$ にのみ興味がある場合は、説明変数 $(X_0, X_1)$ の多重共線性は無視してモデルに含めてもいいことがわかりました。

サンプルサイズとOLS推定量の信頼度

f:id:dropout009:20210722194757p:plain

次に、相関係数 $\rho$ を0.9で固定したままサンプルサイズが変化した場合のOLS推定量の分散を可視化したものが上図になります。
強い多重共線性があるぶん $(\beta_0, \beta_1)$ の信頼度は高めになっていますが、それでもサンプルサイズを大きくれば分散が小さくなっていく様子が見て取れます。
逆に言うと、興味のある説明変数に多重共線性が存在している場合は、できるだけたくさんデータを集める必要があることがわかります。

リッジ推定量で推定量の信頼性を高める

リッジ推定量の導入

ここまで、強い多重共線性が存在すると回帰係数の推定が安定せずOLS推定量 $\hbeta$ の信頼度が下がる（分散が大きくなる）ことを、数式とシミュレーションの両面から見てきました。
推定量の信頼度が低いと、回帰分析を用いた意思決定の信頼度が下がることに繋がります。

そこで、推定量の分散を抑える手法として、リッジ回帰（Redge Regression）という手法が知られています。
この手法では、最小二乗法を行う際の損失関数に、 $\beta$ が大きいほど強い罰則を与える罰則項を加えます。
この罰則によって、推定量は極端に大きな値を取らないような制限がかかり、推定が安定します。

\begin{align}
\hbeta(\lambda) &= \arg\min_{\beta} \paren{\vY - \vX\beta}'\paren{\vY - \vX\beta} + \lambda \beta'\beta\\
&= \inv{\vX'\vX + \lambda \vI_J}\vX'\vY
\end{align}

このような罰則を加えた推定量はリッジ推定量と呼ばれています*3。
ここで、 $\lambda$ は罰則の強さを表しています。
$\beta'\beta = \|\beta\|^2_2$ はL2ノルムによる罰則と解釈できることから、これはL2正則化とも呼ばれています。

OLS推定量と比較して、 $\lambda \vI_J$ の項目が分母にある分、リッジ推定量のほうが（絶対値でみて）小さい値になります。
$\lambda$ が大きいほど強い罰則がかかり、 $\beta$ が0方向に引っ張られます。
実際 $\lambda$ を無限大に飛ばすと推定量は0になります。
逆に、 $\lambda = 0$ のときは、リッジ推定量はOLS推定量と一致します。

リッジ推定量の性質

それでは、リッジ推定量の性質を確認するため、その期待値と分散を計算します。

変換行列の準備

後の話を簡単にするため、OLS推定量をリッジ推定量に変換する行列 $\mW$ を定義しておきます。

\begin{align}
\mW\hbeta &=\hbeta(\lambda)
\end{align}

行列 $\mW$ の中身を知りたいので、OLS推定量とリッジ推定量を代入します。

\begin{align}
\mW\hbeta &=\hbeta(\lambda) \\
\mW \inv{\vX'\vX}\vX'\vY&= \inv{\vX'\vX + \lambda \vI_J}\vX'\vY
\end{align}

両辺に $\inv{\vX'\vY}\paren{\vX'\vX}$ を右からかけてあげると $\mW$ の中身がわかります。

\begin{align}
\mW \inv{\vX'\vX}\vX'\vY\inv{\vX'\vY}\paren{\vX'\vX} &= \inv{\vX'\vX + \lambda \vI_J}\vX'\vY\inv{\vX'\vY}\paren{\vX'\vX}\\
\mW&= \inv{\vX'\vX + \lambda \vI_J}\paren{\vX'\vX}
\end{align}

リッジ推定量の期待値

さて、この変換行列 $\mW$ を用いてリッジ推定量の期待値を計算します。

\begin{align}
\E{\hbeta(\lambda) \mid \vX}
&= \E{\mW\hbeta \mid \vX}\\
&= \mW\E{\hbeta \mid \vX}\\
&= \inv{\vX'\vX + \lambda \vI_J}\paren{\vX'\vX}\beta\\
&\leqslant \beta
\end{align}

OLS推定量とは異なり、リッジ推定量の期待値は真の回帰係数 $\beta$ と一致しません。
分母の $\lambda \vI_J$ の分だけ0方向にバイアスがかかることがわかります。
よって、罰則の強さ $\lambda$ を大きくすればするほどバイアスは大きくなります。

推定量にバイアスがかかるのはあまりうれしくない性質です。
ただ、バイアスの方向がゼロに向かうのは、実務的にはそんなに悪くない性質だと思っています。
というのも、ゼロ方向にバイアスがかかるというのは、説明変数が目的変数に与える効果を「過小評価」するという話なので、リッジ回帰で過小評価されていてもなお十分に効果があるなら、保守的に見てもそのくらいの効果がある可能性が高い、という判断が可能になるからです。

リッジ推定量の分散

次に、リッジ推定量の分散について確認します。

$\begin{align} \var{\hbeta(\lambda) \mid \vX} &= \var{\mW\hbeta \mid \vX}\\ &= \mW\var{\hbeta \mid \vX}\mW'\\ &= \inv{\vX'\vX + \lambda \vI_J}\paren{\vX'\vX}\inv{\vX'\vX}\sigma^2\paren{\vX'\vX}\inv{\vX'\vX + \lambda \vI_J}\\ &= \inv{\vX'\vX + \lambda \vI_J}\paren{\vX'\vX}\inv{\vX'\vX + \lambda \vI_J}\sigma^2 \end{align}$

$\mW$ は分母のほうが大きいので、リッジ推定量の分散はOLS推定量の分散より小さくなることがわかります。また、 $\lambda$ を大きくすれば分散が小さくなることも見て取れます。

まとめると、リッジ推定量は、バイアスがかかることを代償に推定量の信頼性を高める手法であると解釈できます。
このバイアスと信頼性の関係はBias-Variance tradeoffとして機械学習や統計学の分野で知られています。

シミュレーションによる確認

リッジ推定量についても、罰則の強さによって期待値と分散がどのように変化するかシミュレーションで確認しておきます。

まずは期待値について確認します。サンプルサイズを200、相関係数を0.99で固定して、罰則の強さ $\lambda$ だけを変化させた場合のリッジ推定量の期待値を可視化します。
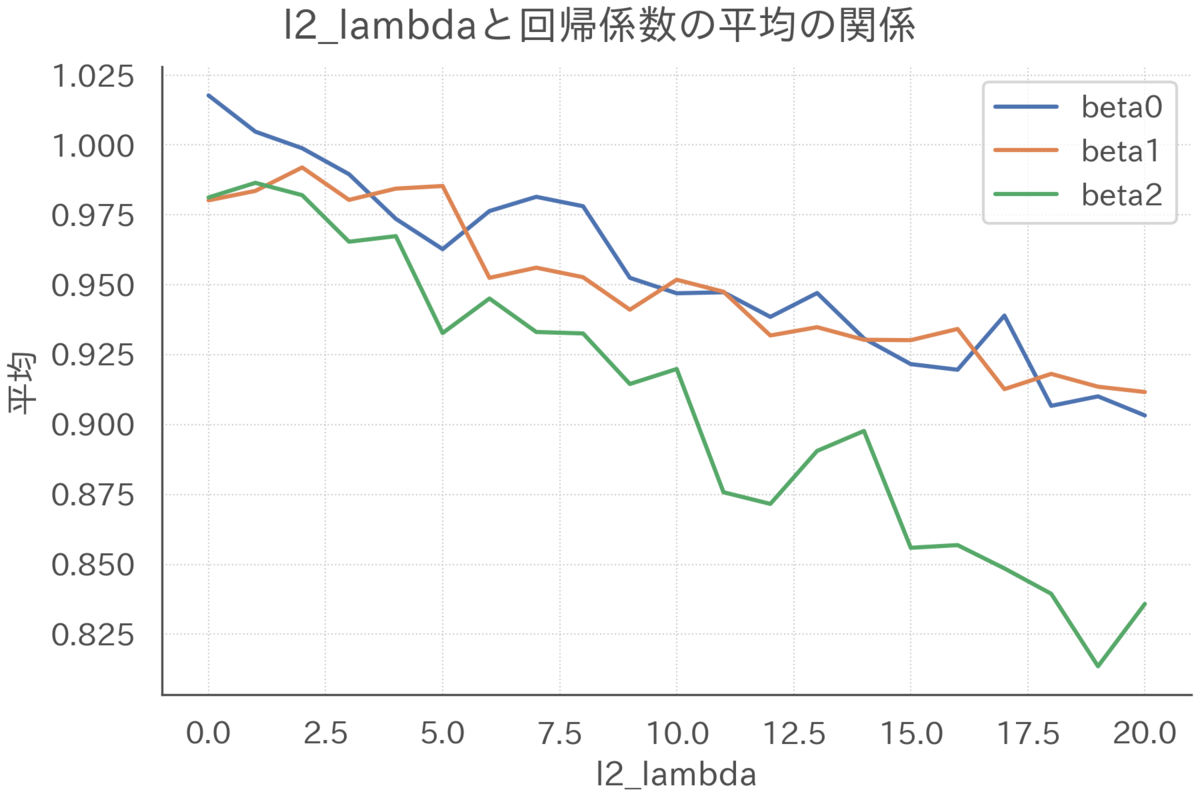
f:id:dropout009:20210722194802p:plain

回帰係数はすべて1だったことを念頭に置いて上図を確認すると、 $\lambda$ を大きくするにつれてリッジ推定量は0方向にひっぱられてバイアスが強くなっていくことがわかります（サンプルサイズが小さく多重共線性が強いので、罰則ゼロのときそもそもあんまりうまく推定できていないことも見て取れます）。

同様の設定でリッジ推定量の分散を確認します。
f:id:dropout009:20210722194808p:plain

罰則を強くすると推定量の分散が小さくなっていく様子が見て取れます。
このように、リッジ推定量はバイアスという犠牲を払って信頼性を高めることができます。

まとめ

この記事では、多重共線性がOLS推定量の信頼性に与える影響について、数式とシミュレーションの両面から確認しました。
大雑把に言うと、完全な多重共線性があるケースを除いて、興味のある説明変数以外の多重共線性はあまり気にしなくて良いことがわかりました。

また、推定量の信頼性を高める手法の一つとして、リッジ推定量を紹介しました。
リッジ推定量はゼロ方向にバイアスがかかりますが、推定量の分散を小さくできることを確認しました。
リッジ推定量には、例えば説明変数の数 $J$ がサンプルサイズ $N$ よりも大きくても推定が可能になるなど、他にも便利な性質がいくつかあります。リッジ推定量の詳細はvan Wieringen(2015)をご確認ください。

この記事で利用したシミュレーションコードは以下になります。
github.com

参考文献

Hansen, Bruce E. "Econometrics." (2021). https://www.ssc.wisc.edu/~bhansen/econometrics/.
van Wieringen, Wessel N. "Lecture notes on ridge regression." arXiv preprint arXiv:1509.09169 (2015).

*1:僕が受講した計量経済学のコースワークは市村英彦先生が担当されていたのですが、講義ノートにはしっかり記述がありました。

*2:Hansen(2011)を特に参考にしています。

*3:リッジ推定量の利点として、完全な多重共線性が存在するケースでも逆行列がとれるので推定が可能になることが挙げられたりしています。それは実際そうなんですが、完全な多重共線性があってしかも回帰係数に興味がある場合はリッジ回帰で対処するのではなく手作業で完全な多重共線性を排除したほうがいいと思います。