2021-08-08

Accumulated Local Effects（ALE）で機械学習モデルを解釈する

$\def\xij{x_{i, j}} \def\vx{\mathbf{x}} \def\vxi{\mathbf{x}_i} \def\vxmj{\mathbf{x}_{\setminus j}} \def\vximj{\mathbf{x}_{i, \setminus j}} \def\vX{\mathbf{X}} \def\vXmj{\mathbf{X}_{\setminus j}} \def\paren#1{\left(#1\right)} \def\brac#1{\left[#1\right]} \def\E#1{\mathbb{E}\brac{#1}} \def\sumi{\sum_{i=1}^N} \def\pd{\mathrm{PD}} \def\ale{\mathrm{ALE}}$

はじめに
Partial Dependence
Marginal Plot
Accumulated Local Effects
まとめ
Appendix：線形回帰モデルの場合
参考文献

この記事をベースにした発表資料です！
speakerdeck.com

はじめに

Random Forestやディープラーニングなどのブラックボックスモデルは、予測性能が高い一方で解釈性が低いというトレードオフを抱えています。
これを克服するために、ブラックボックスモデルに後から解釈性を与える「機械学習の解釈手法」が急速に開発されています。
機械学習の解釈手法を援用することで、高い予測性能を維持しながらモデルの振る舞いを解釈することができるようになります。

機械学習の解釈手法として、代表的な手法のひとつにPartial Dependence（PD）があります。
これは、モデルに投入した特徴量とモデルの予測値の関係を可視化する手法です。
PDを用いることで、特徴量の値が大きくなるとモデルの予測値は大きくなるのか、その関係は線形なのか非線形なのかといった振る舞いを知ることが出来ます。

PDは特徴量とモデルの予測値の関係を知る上で便利な手法ですが、もちろん限界があります。
PDがあまりうまく機能しない代表的な例として、モデルに投入した特徴量が強く相関する場合が挙げられます。
この記事では、特徴量に相関があるとなぜPDがうまく機能しないのかを説明し、この状況でうまく機能する手法としてAccumulated Local Effects（ALE）を紹介します。

この記事では実際にPythonでALEのアルゴリズムを実装することを通じてALEの振る舞いを確認していきます。
一方で、ALEの数学的な側面にはあまり触れません。
ALEについてより詳しく知りたい場合は元論文のApley and Zhu(2020)をご確認ください。

また、この記事では、PDについてはある程度知識があるものとしてALEを解説します。
PDについての詳細は、拙著「機械学習を解釈する技術」やMolner(2019)を参考にして下さい。
「機械学習を解釈する技術」は、この記事と同じように、実際にPythonでアルゴリズムを実装することを通じて機械学習の解釈手法を理解することを目指しています。

機械学習を解釈する技術〜予測力と説明力を両立する実践テクニック

作者:森下光之助
技術評論社

Amazon

Partial Dependence

Partial Dependenceがどのような場合にうまく機能して、どのような場合に機能しないのかを確認するため、シミュレーションデータを用いてPDの振る舞いを確認します。
具体例で考えたほうがわかりやすいので、特徴量が $(X_0, X_1)$ の2つのケースを考えます。
真の関数形は $f(X_0, X_1) = X_0 + X_1^2$ となっていて、それにノイズ $\epsilon$ が乗ってアウトカム $Y$ が観測されているとします。

\begin{align}
Y &= X_0 + X_1^2 + \epsilon
\end{align}

# いろんなところで使うので真の関数形を定義しておく
def f(X: np.ndarray) -> np.ndarray:
    """真の関数形：f(X0, X1) = X0 + X1^2"""
    return X[:, 0] + X[:, 1] ** 2

特徴量が独立の場合

まずは、PDがうまくいくケースとして、特徴量 $(X_0, X_1)$ が無相関であるケースを考えましょう。
シミュレーションデータを生成する関数generate_simulation_data()を定義して、データを生成します。
特徴量 $(X_0, X_1)$ は区間 $[0, 1$ ]の一様分布から生成され、ノイズ $\epsilon$ は平均が0で標準偏差がsigma_eの正規分布から生成されるとします。
あとで特徴量 $(X_0, X_1)$ が相関するケースを考えるので、相関係数rhoで相関の強さを調整できるようにしておきます。

def generate_simulation_data(
    N: int = 10000,
    rho: float = 0.0,
    sigma_e: float = 0.01,
    f: Callable[[np.ndarray], np.ndarray] = f,
) -> tuple[np.ndarray, np.ndarray]:
    """シミュレーションデータを生成する関数"""

    # 区間[0, 1]の一様分布に従って、しかも相関する特徴量が作りたい
    # 正規分布を使って相関する特徴量を作る
    mu = np.array([0, 0])
    Sigma = np.array([[1, rho], [rho, 1]])
    X = np.random.multivariate_normal(mu, Sigma, N)
    for j in range(2):
        # 正規分布の確率密度関数を噛ませると区間[0, 1]の一様分布に従うようになる
        X[:, j] = sp.stats.norm().cdf(X[:, j])

    # ノイズ
    e = np.random.normal(0, sigma_e, N)

    # 目的変数
    y = f(X) + e

    return X, y


# 相関なしのシミュレーションデータを生成
X_indep, y_indep = generate_simulation_data()

数式による確認

いま、特徴量 $X_0$ とモデルの予測値の関係を知りたいとします。
PDでは、興味のある特徴量 $X_0$ 以外の特徴量に関しては期待値をとることで、特徴量 $X_0$ とモデルの予測値の関係にのみ焦点を当てます。
この操作は周辺化と呼ばれています。
具体的に、モデルが真の関数形 $f(X_0, X_1) = X_0 + X_1^2$ を完璧に学習できているとすると、PDの理論値は以下になります。

\begin{align}
\pd_0(x_0)
&= \E{f(x_0, X_1)}\\
&= \E{x_0 + X_1^2}\\
&= x_0 + \E{X_1^2}\\
&= x_0 + \frac{1}{3}
\end{align}

ここで、 $\E{X_1^2} = 1/3$ は特徴量 $X_1$ が区間 $[0, 1$ ]の一様分布に従うことを利用しています。
$x_0$ の係数は1であり、特徴量 $X_0$ が1単位大きくなるとモデルの予測値が1大きくなるという関係を、PDはうまく捉えられることがわかります。
特徴量 $X_1$ についても同様にしてPDの理論値を計算することができます。

\begin{align}
\pd_1(x_1)
&= \E{f(X_0, x_1)}\\
&= \E{X_0 + x_1^2}\\
&= \E{X_0} + x_1^2\\
&= \frac{1}{2} + x_1^2
\end{align}

ここで、 $\E{X_0} = 1/2$ は特徴量 $X_0$ が区間 $[0, 1$ ]の一様分布に従うことを利用しています。
こちらも、特徴量 $X_1$ に関する非線形な関係をPDで捉えることができていることがわかります。

もう少し一般的に言うと、興味のある特徴量を $X_j$ とし、それ以外の特徴量を $\vXmj = (X_1, \dots, X_{j-1}, X_{j+1}, \dots, X_J)$ とすると、PDは

\begin{align}
\pd_j(x_j) = \E{f(x_j, \vXmj)}
\end{align}

と表記できます。

もちろん期待値というのは理論的な存在なので、実際にPDを知るためにはデータから推定する必要があります。
推定を行うには、興味のある特徴量 $X_j$ の値を全てのインスタンスで特定の値 $x_j$ に置き換えて、その平均値をとります。

\begin{align}
\widehat{\pd}_j(x_j) = \frac{1}{N}\sumi f(x_j, \vximj)
\end{align}

この操作を $X_j$ の最小値から最大値までちょっとずつ $x_j$ の値を変化させながら何度も行います。
PDの変化をみていくことで、特徴量とモデルの予測値の平均的な関係を知ることが出来ます。

PDの実装

実際にPDのアルゴリズムをPythonで実装すると以下のようになります。
このPartialDependencePlotクラスでは、

特徴量の値を置き換えて予測を行い、結果を平均する_predict_average()メソッド
それを用いて各特徴量に対するPDを計算する_estimate_relationship()メソッド
すべての特徴量に対してPDの結果を可視化するplot()メソッド

を実装しています。

@dataclass
class PartialDependence:
    """Partial Dependence (PD)

    Args:
        estimator: 学習済みモデル
        X: 特徴量
    """

    estimator: Any
    X: np.ndarray

    def _predict_average(self, X: np.ndarray, j: int, xj: float) -> np.ndarray:
        """特徴量の値を置き換えて予測を行い、結果を平均する

        Args:
            j: 値を置き換える特徴量のインデックス
            xj: 置き換える値
        """

        # 特徴量の値を置き換える際、元データが上書きされないようコピー
        # 特徴量の値を置き換えて予測し、平均をとって返す
        X_replaced = X.copy()
        X_replaced[:, j] = xj

        return self.estimator.predict(X_replaced).mean()

    def _estimate_relationship(
        self, j: int, n_grid: int = 30
    ) -> tuple[np.ndarray, np.ndarray]:
        """PDを求める

        Args:
            j: PDを計算したい特徴量のインデックス
            n_grid: グリッドを何分割するか
        Returns:
            特徴量の値とその場合のPD
        """

        # ターゲットの変数を、取りうる値の最大値から最小値まで動かせるようにする
        xjs = np.linspace(self.X[:, j].min(), self.X[:, j].max(), num=n_grid)

        # インスタンスごとの予測値を平均
        partial_dependence = np.array(
            [self._predict_average(self.X, j, xj) for xj in xjs]
        )

        return (xjs, partial_dependence)

    def plot(
        self,
        fs: list[Callable[[np.ndarray], np.ndarray]],
        ylabel: str | None = None,
        title: str | None = None,
    ) -> None:
        """すべての特徴量に対して可視化を行う

        Args:
            fs: 理論的な関係を表す関数。特徴量の数だけ必要
            ylabel: 縦軸のラベル
            title: 画像のタイトル
        """

        J = len(fs)  # 特徴量の数
        # J個グラフを作成
        fig, axes = plt.subplots(nrows=1, ncols=J, figsize=(4 * J, 4))
        for j in range(J):
            # 推定された特徴量と予測値の関係
            xjs, pred = self._estimate_relationship(j)

            # 理論的な関係
            y = fs[j](xjs)

            # 理論的な関係を可視化
            axes[j].plot(xjs, y, zorder=1, c=".7", label="理論的な関係")

            # 推定された関係を可視化
            axes[j].plot(xjs, pred, zorder=2, label="推定された関係")

            axes[j].set(xlabel=f"X{j}", ylabel=ylabel)
            axes[j].legend()

        fig.suptitle(title)
        fig.show()

実際にRandom Forestを用いて予測モデルを構築し、PartialDependenceクラスを用いてPDを適用してみましょう。

# Random Forestで予測モデルを構築
rf_indep = RandomForestRegressor(n_jobs=-1, random_state=42).fit(X_indep, y_indep)

# インスタンスを作成
pd_indep = PartialDependence(estimator=rf_indep, X=X_indep)

# PDを可視化
# fsには理論的な関係を与える
fs = [lambda x: x + 1 / 3, lambda x: x ** 2 + 0.5]
pd_indep.plot(
    fs=fs, ylabel="Partial Dependence", title="理論的な関係とPDで推定された関係の比較（特徴量の相関なし）"
)

f:id:dropout009:20210808015712p:plain

重なっていてほぼ見えていませんが、グレーの線が理論的な関係、青い線がParital Dependenceによって推定された関係を表しています。
ふたつの線はほぼ一致しており、特徴量 $(X_0, X_1)$ 共に、PDはうまく理論的な関係を捉えられていることが分かります。

特徴量が相関する場合

次に、特徴量が強く相関する場合を考えます。
特徴量 $(X_0, X_1)$ の相関係数を0.99としてシミュレーションデータを生成し、Random Forestで学習を行います。

# 特徴量が相関している場合のデータを生成
X, y = generate_simulation_data(rho=0.99)

# Random Forestで予測モデルを構築
rf = RandomForestRegressor(n_jobs=-1, random_state=42).fit(X, y)

PDで特徴量とモデルの予測値の関係を確認します。

# インスタンスを作成
pd = PartialDependence(estimator=rf, X=X)

# PDを可視化
fs = [lambda x: x + 1 / 3, lambda x: x ** 2 + 0.5]
pd.plot(fs=fs, ylabel="Partial Dependence", title="理論的な関係とPDで推定された関係の比較（特徴量が強く相関）")

f:id:dropout009:20210808015717p:plain

特徴量に相関がない場合とは異なり、特徴量に強い相関がある場合は、特徴量 $(X_0, X_1)$ 共にPDによる推定結果は理論的な関係とズレが生じています。

PDがうまく機能しない原因

特徴量が相関するとなぜPDがうまく機能しないのでしょうか。
結論を先に述べると、特徴量が相関している場合、いわゆる「外挿」の問題が起きてしまうことが原因です。
これを確認するために、特徴量 $(X_0, X_1)$ の散布図を作成します。
また、特徴量 $(X_0, X_1)$ に対する理論的なアウトカム $Y$ の値が見て取れるように、等高線も可視化しておきます。

def draw_contour(
    ax: plt.Axes,
    X: np.ndarray,
    f1: Callable[[np.ndarray], np.ndarray],  # 等高線引くための関数
    f2: Callable[[np.ndarray], np.ndarray] | None = None,  # 2つまで指定可能
    xlabel: str | None = None,
    ylabel: str | None = None,
    title: str | None = None,
    cmaps: list[str] = ["viridis"],
) -> plt.Axes:
    """等高線プロット"""

    x = np.linspace(0, 1, num=50)

    ax.scatter(X[:, 0], X[:, 1], c=".8")

    z = f1(cartesian([x, x])).reshape(50, 50, order="F")
    CS = ax.contour(x, x, z, levels=10, cmap=cmaps[0])
    ax.clabel(CS, fmt="%1.2f")

    if f2 is not None:
        z = f2(cartesian([x, x])).reshape(50, 50, order="F")
        CS = ax.contour(x, x, z, levels=10, cmap=cmaps[1])
        ax.clabel(CS, fmt="%1.2f")

    ax.set(xlabel=xlabel, ylabel=ylabel, title=title)


def draw_contours(X: np.ndarray, model: Any, title: str | None = None) -> None:
    """等高線プロットを3つまとめる関数"""
    fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(4 * 3, 4))
    draw_contour(
        ax=axes[0],
        X=X,
        f1=f,
        xlabel="X0",
        ylabel="X1",
        title="特徴量(X0, X1)と理論値の関係",
    )
    draw_contour(
        ax=axes[1],
        X=X,
        f1=model.predict,
        xlabel="X0",
        ylabel="X1",
        cmaps=["magma"],
        title="特徴量(X0, X1)と予測値の関係",
    )
    draw_contour(
        ax=axes[2],
        X=X,
        f1=f,
        f2=model.predict,
        xlabel="X0",
        ylabel="X1",
        cmaps=["viridis", "magma"],
        title="特徴量(X0, X1)と理論値/予測値の関係",
    )

    fig.suptitle(title)
    fig.show()

まずは特徴量が相関していないケースを可視化します。

# 特徴量が相関していない場合の理論値と予測値の関係を可視化
draw_contours(
    X=X_indep, model=rf_indep, title="理論値とRandom Forestの予測値の関係（特徴量が強く相関していない場合）"
)

f:id:dropout009:20210808015722p:plain

データはすべての範囲で均等に存在し、また理論値とモデルの予測値はすべての範囲で一致していることがわかります。

次に、特徴量が強く相関してる場合を可視化します。

# 特徴量が相関している場合の理論値と予測値の関係を可視化
draw_contours(X=X, model=rf, title="理論値とRandom Forestの予測値の関係（特徴量が強く相関している場合）")

f:id:dropout009:20210808015729p:plain

特徴量が相関しているので、画像の左上と右下の範囲にはデータが存在しません。
また、データの存在しない左上と右下の範囲では、Random Forestの予測値は理論的な値とズレが生じています。
これは外挿と呼ばれている問題で、訓練データに存在しない範囲での予測は一般にあまりうまくいきません。

この外挿問題がPDに悪影響を与えます。
特徴量 $X_0$ に対するPDを考えます。
$X_0 = 0.9$ のときのPDは以下のように全インスタンスの予測値を平均して求めていました。

\begin{align}
\widehat{\pd}_0(0.9) = \frac{1}{N}\sumi f(0.9, x_{i, 1})
\end{align}

ここで問題になるのは、 $X_0 = 0.9$ のときは $X_1$ が0から0.8くらいまでのインスタンスは実際には存在しないことです。
よって、実際には $(X_0, X_1) = (0.9, 0.2)$ のような組み合わせのインスタンスは存在しないにもかかわらず、無理やり $f(0.9, 0.2)$ という予測を行い、その結果を平均していることになります。
もちろん、このような特徴量の「ありえない」組み合わせに対してもうまく予測が行えるなら問題はないのですが、実際はこのような範囲での予測は往々にして精度が悪く、結果としてPDは理論的な関係をうまく捉えることができません。

特徴量に相関がある場合にPDが理論的な関係を復元できないことは事実ですが、データには存在しない特徴量の組み合わせに対してモデルがおかしな予測値を出すこともまた事実であり、その意味ではPDは「特徴量とモデルの予測値の関係」を捉えていると言えるかもしれません。
しかし、モデルの振る舞いを解釈するという観点では、データに存在しない特徴量の組み合わせに対するモデルの振る舞いではなく、データがきちんと存在する部分でのモデルの振る舞いを解釈したいというのが通常のモチベーションでしょう。
このモチベーションにおいては、特徴量が相関する場合はPDの結果をそのまま解釈するのは危険が伴います。

Marginal Plot

Marginal Plotの数式

PDがうまく機能しない原因は、データには存在しないような組み合わせの特徴量に対する予測値を使ってしまうことでした。
ということは、データが存在する範囲だけで期待値をとってあげればこの問題を回避できそうな気がします。
つまり、周辺分布 $p(\vxmj)$ を使って期待値

\begin{align}
\E{f(x_j, \vXmj)} = \int f(x_j, \vxmj)p(\vxmj)d\vxmj
\end{align}

をとるのではなく、条件付き分布 $p(\vxmj | x_j)$ を使って条件付き期待値

\begin{align}
\E{f(x_j, \vXmj)\mid X_j = x_j} = \int f(x_j, \vxmj)p(\vxmj | x_j)d\vxmj
\end{align}

をとればうまくいくかもしれません。
この条件付き期待値を用いた可視化はMarginal Plotと呼ばれています。

残念なことに、この手法は理論的な関係をうまく復元できないことがわかっています。
極端な例として、 $f(X_0, X_1) = X_0 + X_1^2$ で、特徴量 $(X_0, X_1)$ が完全に相関しているケース、つまり $X_0 = X_1$ のケースを考えます。
このとき、特徴量 $X_0$ に対するMarginal Plotの理論値は以下になります。

\begin{align}
\mathrm{M}_0(x_0)
&= \E{f(x_0, X_1) \mid X_0 = x_0}\\
&= \E{x_0 + X_1^2 \mid X_0 = x_0}\\
&= x_0 + \E{X_1^2 \mid X_0 = x_0}\\
&= x_0 + x_0^2
\end{align}

同様に、特徴量 $X_0$ に対する理論値は以下になります。

\begin{align}
\mathrm{M}_1(x_1)
&= \E{f(X_0, x_1) \mid X_1 = x_1}\\
&= \E{X_0 + x_1^2\mid X_1 = x_1}\\
&= \E{x_0\mid X_1 = x_1} + x_1^2\\
&= x_1 + x_1^2
\end{align}

ここから分かるように、特徴量が完全に相関している場合、Marginal Plotでは特徴量 $(X_0, X_1)$ の効果が完全に混ざってしまっています。
話を簡単にするために特徴量が完全に相関しているという極端なケースを考えましたが、一般的に、相関が強いほど特徴量の効果が混ざり合う度合いが強くなります。

Marginal Plotのアルゴリズム

理論的には、Marginal Plotはあまりうまく行かなさそうなことがわかりましたが、一応、Marginal Plotを作成するためのアルゴリズムを考えてみましょう。
条件付き分布 $p(x_j \mid \vxmj)$ はちゃんと推定しようとすると難しいですが、手っ取り早いやり方として、特徴量 $X_j$ の値の範囲をいくつかのブロックに分割して、そこに含まれるインスタンスのみを利用して予測値を出し、平均することにします。

つまり、Marginal Plotを計算するアルゴリズムは以下になります。

（１）特徴量 $X_j$ の値の取りうる範囲を $[x_j^{(0)}, x_j^{(1)}),\; [x_j^{(1)}, x_j^{(2)}),\; \dots,\; [x_j^{(k-1)}, x_j^{(k)})\dots,\;[x_j^{(K-1)}, x_j^{(K)}$ ]のように $K$ 個のブロックに分割する。ここで、 $x_j^{(0)}$ と $x_j^{(K)}$ は特徴量 $X_j$ が取りうる値の最小値と最大値を表す。範囲が $[x_j^{(k-1)}, x_j^{(k)})$ であるブロックをブロック $k$ と呼ぶ
（２）ブロック $k$ に対して、特徴量 $X_j$ の値がそのブロックの区間 $[x_j^{(k-1)}, x_j^{(k)})$ に入っているインスタンスを抜き出してきて、 $X_j$ の値を $\frac{1}{2}\paren{x_j^{(k-1)} + x_j^{(k)}}$ に置き換えたの場合の予測値を求めて平均する。つまり、

$\begin{align} \frac{1}{N^{(k)}} \sum_{i: x_{j}^{(k-1)} \leq x_{i, j} < x_{j}^{(k)}} f\paren{\frac{x_j^{(k-1)} + x_j^{(k)}}{2}, \vximj} \end{align}$

を計算する。ここで、 $N^{(k)}$ はブロック $k$ に含まれるインスタンスの総数を表す

（３）上記の操作を全ての $k = 1, \dots, K$ に対して行う

例えば、特徴量 $X_0$ は区間 $[0, 1$ ]に分布しているので、これを $[0, 0.1),\; [0.1, 0.2),\; \dots,\; [0.9, 1$ ]に分割します。区間 $[0.1, 0.2)$ について考えると、特徴量 $X_0$ の値が区間 $[0.1, 0.2)$ に含まれるインスタンスを持ってきて、 $X_0$ の値を0.15に置き換えたのときの予測値を出し、平均します。

Maginal Plotの実装

実際にMarginal Plotのアルゴリズムを実装してみましょう。
先程実装したPartialDependenceクラスを継承して、_estimate_relationship()メソッドを上記のアルゴリズムでオーバーライドすればOKです。

class Marginal(PartialDependence):
    """Marginal Plot"""

    def _estimate_relationship(
        self, j: int, n_grid: int = 30
    ) -> tuple[np.ndarray, np.ndarray]:
        """Marginal Predictionを求める

        Args:
            j: Marginal Predictionを計算したい特徴量のインデックス
            n_grid: グリッドを何分割するか
        Returns:
            特徴量の値とその場合のMarginal Prediction
        """

        # ターゲットの変数を、取りうる値の最大値から最小値まで動かせるようにする
        # 全てのブロックに同じ数だけのインスタンスが入るようにする
        xjks = np.quantile(self.X[:, j], q=np.arange(0, 1, 1 / n_grid))

        # ブロックごとに平均的な予測値を求める
        marginals = np.zeros(n_grid)
        for k in range(1, n_grid):
            mask = (self.X[:, j] >= xjks[k - 1]) & (self.X[:, j] <= xjks[k])

            marginals[k] = self._predict_average(
                self.X[mask], j, (xjks[k - 1] + xjks[k]) / 2
            )

        return (xjks, marginals)

実装したMarginalクラスを使って、Marginal Plotを作成します。

# インスタンスを作成
m = Marginal(estimator=rf, X=X)

# 可視化
fs = [lambda x: x, lambda x: x ** 2]
m.plot(fs=fs, ylabel="Marginal Plot", title="理論的な関係とMarginalで推定された関係の比較（特徴量の相関あり）")

f:id:dropout009:20210808015735p:plain

数式でも確認したように、特徴量 $(X_0, X_1)$ のどちらも関係が $x + x^2$ として可視化されています。
今回知りたいのは個別の特徴量と予測値の関係なので、特徴量 $(X_0, X_1)$ の効果が混ざってしまうMarginal Plotはこの用途にはあまり適しているは言えません。

Accumulated Local Effects

ALEのアイデア

さて、PDのように期待値をとってもだめ、Marginal Plotのように条件付き期待値をとってもだめだとすると、特徴量が相関する場合に特徴量と予測値の関係をどうやって解釈すればよいのでしょうか。

実は、この問題を解決する手法として、Accumulated Local Effects（ALE）が提案されています。

ALEは、Marginal Plotと同じく、特徴量 $X_j$ の値の範囲をいくつかのブロックに分割して、そこに含まれるインスタンスのみを対象にする手法です。
ただし、Marginal Plotはその区間での「平均的な予測値」に注目していましたが、ALEではその区間の両端での「予測値の差分」に注目します。

何を言っているかわからないと思うので、もう少し丁寧に説明させてください。
話を簡単にするために、下図のような特徴量がひとつのケースを考えます。

f:id:dropout009:20210808020659p:plain

特徴量 $X$ の区間を $[x^{(0)}, x^{(1)}),\;[x^{(1)}, x^{(2)}),\;[x^{(2)}, x^{(3)}), \dots$ と分割しています。
ここで、区間 $[x^{(0)}, x^{(1)})$ に注目すると、両端での予測値の差分は $f(x^{(1)}) - f(x^{(0)})$ で求まります。
同様にして、区間 $[x^{(1)}, x^{(2)})$ での予測値の差分は $f(x^{(2)}) - f(x^{(1)})$ 、区間 $[x^{(2)}, x^{(3)})$ での予測値の差分は $f(x^{(3)}) - f(x^{(2)})$ のように計算していくことができます。
また、このようにして求めた区間ごとの予測値の差分 $f(x^{(k)}) - f(x^{(k-1)})$ を累積（Accumulate）していくことで、理論的な関係を復元することができそうです。
区間ごとの予測値の差分を、この区間における特徴量が与えた効果（Local Efffect）と解釈し、その効果を累積（Accumulate）するので、この手法はAccumulated Local Effectsと呼ばれています。

さて、ALEが特徴量と予測値の関係を捉えられそうな雰囲気がでてきましたが、これは特徴量が相関するケースでもうまく機能するのでしょうか。
これまで考えたきたシミュレーションデータのように、特徴量 $(X_0, X_1)$ に強い相関が見られるケースを考えます。
特徴量 $X_0$ とモデルの予測値の関係を解釈したいとします。
特徴量がひとつのケースと同様に、特徴量 $X_0$ の区間を $[x^{(0)}_0, x^{(1)}_0),\;[x^{(1)}_0, x^{(2)}_0),\;[x^{(2)}_0, x^{(3)}_0), \dots$ と分割します。
あとは各区間の両端での予測値の差分を計算すると、その区間で特徴量 $X_0$ の効果が計算できます。

f:id:dropout009:20210808020702p:plain

具体的に、上図のような状況を考えます。
上図では、区間 $[x^{(1)}_0, x^{(2)}_0)$ に含まれているインスタンスを4つ抜き出しています（上から順にインスタンス0、インスタンス1、インスタンス2、インスタンス3とします）。

これらのインスタンスに対して、ALEは下図のような計算を行います。

f:id:dropout009:20210808020707p:plain

区間 $[x^{(1)}_0, x^{(2)}_0)$ に含まれているインスタンスに対して、そのインスタンスの特徴量 $X_1$ の値は固定しておいて、特徴量 $X_0$ のみ区間の両端の値に置き換えて予測値の差分を計算します。

\begin{align}
f(x_0^{(2)}, x_{i, 1}) - f(x_0^{(1)}, x_{i, 1})
\end{align}

これをこの区間に含まれるすべてのインスタンスに対して行い、結果を平均することで、この区間における特徴量 $X_0$ のLocal Effectを計算することができます。

ALEはうまく機能するのか

さて、ALEの計算方法はわかりましたが、特徴量が相関するケースでもALEはうまく機能するのでしょうか。
これを確認するため、具体的に $f(X_0, X_1) = X_0 + X_1^2$ のケースを考えます。
この場合、インスタンス $i$ の特徴量 $X_0$ に関するLocal Effectは

\begin{align}
f(x_0^{(2)}, x_{i, 1}) - f(x_0^{(1)}, x_{i, 1})
&= \paren{x_0^{(2)} + x_{i, 1}^2} - \paren{x_0^{(1)} + x_{i, 1}^2}\\
&= x_0^{(2)} - x_0^{(1)}
\end{align}

であり、特徴量 $X_1$ の影響を完全に消し飛ばして特徴量 $X_0$ の効果を純粋に取り出せていることがわかります（特徴量 $X_0$ が1大きくなるとモデルの予測値も1大きくなる）。
また、ALEの計算には区間 $[x^{(1)}_0, x^{(2)}_0)$ に含まれているインスタンスのみを用いるため、PDで起きていたような外挿の影響も受けません。
よって、特徴量が相関するケースでも、ALEは特徴量とモデルの予測値の関係をうまく捉えることができそうです。

ただし、この結果は $f(X_0, X_1) = f_0(X_0) + f_1(X_1)$ のように交互作用のない場合にのみ通用します。
交互作用がある場合にALEがどのように振る舞うかはApley and Zhu(2020)や"Limitations of Interpretable Machine Learning Methods"をご確認ください。

ALEのアルゴリズム

特徴量が2つのケースを用いてALEのアイデアを把握できたので、特徴量が $J$ 個の場合に一般化したアルゴリズムも確認しておきます。
記号がややこしくなっていますが、やっていることは先程の特徴量が2つの場合と同じです。

（１）特徴量 $X_j$ の値の取りうる範囲を $[x_j^{(0)}, x_j^{(1)}),\; [x_j^{(1)}, x_j^{(2)}),\; \dots,\; [x_j^{(k-1)}, x_j^{(k)})\dots,\;[x_j^{(K-1)}, x_j^{(K)}$ ]のように $K$ 個のブロックに分割する。ここで、 $x_j^{(0)}$ と $x_j^{(K)}$ は特徴量 $X_j$ が取りうる値の最小値と最大値を表す。範囲が $[x_j^{(k-1)}, x_j^{(k)})$ であるブロックをブロック $k$ と呼ぶ
（２）ブロック $k$ に対して、特徴量 $X_j$ の値がそのブロックの区間 $[x_j^{(k-1)}, x_j^{(k)})$ に入っているインスタンスを抜き出してきて、 $X_j$ の値を $x_j^{(k-1)}$ と $x_j^{(k)}$ に置き換えたの場合の予測値の差分を求めて平均する。つまり、

$\begin{align} \frac{1}{N^{(k)}} \sum_{i: x_{j}^{(k-1)} \leq x_{i, j} < x_{j}^{(k)}} \paren{f\paren{x_j^{(k)}, \vximj} - f\paren{x_j^{(k-1)}, \vximj}} \end{align}$

を計算する。ここで、 $N^{(k)}$ はブロック $k$ に含まれるインスタンスの総数を表す。これをLocal Effectと呼ぶ

（３）上記の操作を全ての $k = 1, \dots, K$ に対して行う
（４）求めたLocal Effectを累積する

ALEの実装

実際にALEのアルゴリズムを実装してみましょう。
これもMarginalクラスと同じく、PartialDependenceクラスを継承して_estimate_relationship()メソッドを上記のアルゴリズムでオーバーライドすればOKです。

class AccumulatedLocalEffects(PartialDependence):
    """Accumulated Local Effects Plot(ALE)"""

    def _estimate_relationship(
        self, j: int, n_grid: int = 30
    ) -> tuple[np.ndarray, np.ndarray]:
        """ALEを求める

        Args:
            j: ALEを計算したい特徴量のインデックス
            n_grid: グリッドを何分割するか
        Returns:
            特徴量の値とその場合のALE
        """

        # ターゲットの変数を、取りうる値の最大値から最小値まで動かせるようにする
        xjks = np.quantile(self.X[:, j], q=np.arange(0, 1, 1 / n_grid))
        
        # 区間ごとに両端での予測値の平均的な差分を求める
        local_effects = np.zeros(n_grid)
        for k in range(1, n_grid):
            mask = (self.X[:, j] >= xjks[k - 1]) & (self.X[:, j] <= xjks[k])

            local_effects[k] = self._predict_average(
                self.X[mask], j, xjks[k]
            ) - self._predict_average(self.X[mask], j, xjks[k - 1])

        accumulated_local_effects = np.cumsum(local_effects)

        return (xjks, accumulated_local_effects)

実装したAccumulatedLocalEffectsクラスを使って、ALEを可視化します。

ale = AccumulatedLocalEffects(estimator=rf, X=X)
fs = [lambda x: x, lambda x: x ** 2]
ale.plot(fs=fs, ylabel="Partial Dependence", title="理論的な関係とALEで推定された関係の比較（特徴量の相関あり）")

f:id:dropout009:20210808015740p:plain

特徴量が強く相関する場合、PDはやMarginal Plotでは理論的な関係をうまく捉えることができませんでしたが、ALEはこの問題を克服できていることがわかります。

ALEの数式

最後に、ALEの数式による表現も確認しておきます。
実際のデータからALEを計算する際には、特徴量 $X_j$ の区間を分割してその中での特徴量 $X_j$ が与える効果を計算し、それを累積していました。
理論的には、この区間を細かくするほどより正確な近似を行うことができるはずです。

特徴量 $X_j$ が微小に変化した際の効果は微分を用いることで表現できます。

\begin{align}
\frac{\partial f(X_j, \vXmj)}{\partial X_j}
\end{align}

$X_j = z_j$ で条件づけた場合の $\partial f(X_j, \vXmj)/\partial X_j$ の期待値を計算することで、 $X_j = z_j$ におけるLocal Effectを知ることができます。

\begin{align}
\E{\frac{\partial f(X_j, \vXmj)}{\partial X_j} \mid X_j = z_j}
\end{align}

このLocal Effectを最小値 $x_j^{(0)}$ から累積していくことで、ALEを求めることができます。
累積は積分で計算できます。

\begin{align}
\ale_j(x_j) = \int_{x_j^{(0)}}^{x_j} \E{\frac{\partial f(X_j, \vXmj)}{\partial X_j} \mid X_j = z_j}dz_j
\end{align}

実際に $f(X_0, X_1) = X_0 + X_1^2$ の場合にALEの理論値を計算してみましょう。
まず、特徴量 $X_0$ に対するALEを求めます。

\begin{align}
\ale_0(x_0)
&= \int_{0}^{x_0} \E{\frac{\partial \paren{X_0 + X_1^2}}{\partial X_0} \mid X_0 = z_0}dz_0\\
&= \int_{0}^{x_0} \E{1 \mid X_0 = z_0}dz_0\\
&= \int_{0}^{x_0} 1dz_0\\
&= x_0
\end{align}

ALEが理論的な関係をうまく捉えられていることがわかります。
次に、特徴量 $X_0$ に対するALEを求めます。

\begin{align}
\ale_1(x_1)
&= \int_{0}^{x_1} \E{\frac{\partial \paren{X_0 + X_1^2}}{\partial X_1} \mid X_1 = z_1}dz_1\\
&= \int_{0}^{x_1} \E{2X_1 \mid X_1 = z_1}dz_1\\
&= \int_{0}^{x_1} 2z_1dz_1\\
&= x_1^2
\end{align}

こちらも同様に、ALEが理論的な関係をうまく捉えられていることがわかります。

まとめ

この記事では、特徴量に相関があるとPDがなぜうまく機能しないのかを説明し、問題を解決する手法としてAccumulated Local Effects（ALE）を紹介しました。

PDは特徴量とモデルの予測値の関係を知ることができる有用な解釈手法だが、特徴量が強く相関する場合はあまりうまく機能しない。データには存在しない特徴量の組み合わせに対して無理やり予測した結果を利用することが原因（外挿問題）
この問題を単純に回避しようとする手法にMarginal Plotがあるが、うまくいかない。Marginal Plotでは相関する特徴量の効果が混ざってしまう
ALEは特徴量が強く相関する場合でも、（データが存在する範囲での）特徴量をとモデルの予測値の関係をうまく解釈することができる

ただし、ALEはあくまで平均的な効果を解釈しており、インスタンスごとの解釈を行うことはできません。
もちろん平均的な効果を知ることは重要ですが、特徴量が予測値に与える影響はインスタンスの属性によって大きく異なる可能性があります。
このようなインスタンスごとの解釈性が必要な場合はIndividual Conditional Expectation（ICE）を用いて解釈を行う必要があります。
ICEについての解説はこの記事では行わないので、森下(2021)やMolnar(2019)をご確認ください。

また、ALEはあくまでもある区間に含まれるインスタンスに対して特徴量が与える影響を累積であることにも注意が必要です。
区間が離れていくごとにインスタンスの属性も異なっていくと考えられるので、ALEの解釈はあまり離れた部分に対して行うのではなく、できるだけ近い範囲で行うことが無難です。

この記事で利用したPythonコードはgithubにアップロードしています。
github.com

Appendix：線形回帰モデルの場合

特徴量が強く相関する場合、データには存在しない特徴量の組み合わせに対して無理やり予測した結果を利用することがPDがうまく機能しない原因でした。
ですので、外挿の場合もうまく予測ができるなら、特徴量が強く相関していてもPDはうまく機能します。

実際にこれを確認するため、Random Forestではなく線形回帰モデルを利用してみましょう。
具体的に、線形回帰モデル

\begin{align}
Y = \beta_0X_0 + \beta_1X_1^2 + \epsilon
\end{align}

を考えます。

class Preprocessor(BaseEstimator, TransformerMixin):
    """特徴量X1を二乗するだけの前処理クラス"""

    def fit(self, X: np.ndarray, y=None):
        # 　特になにもしない
        return self

    def transform(self, X: np.ndarray) -> np.ndarray:
        _X = X.copy()  # 直接の書き換えが起きないように
        _X[:, 1] = _X[:, 1] ** 2  # 特徴量X1を二乗した値にする

        return _X


# 線形回帰モデルを用いて予測モデルを構築
lm = Pipeline(
    steps=[
        ("prep", Preprocessor()),
        ("lm", LinearRegression()),
    ]
).fit(X, y)

この線形回帰モデルの予測値と理論値と比較してみます。

# 線形回帰モデルの予測値と理論値の比較
draw_contours(X=X, model=lm, title="理論値と線形回帰モデルの予測値（特徴量が強く相関している場合）")

f:id:dropout009:20210808015746p:plain

この線形回帰モデルはデータの存在しない範囲においても理論的な関係を完璧に学習できていて、外挿がうまくいっていることがわかります。

この場合、PDでも理論的な関係を復元することができます。

# インスタンスを作成
pd = PartialDependence(lm, X)

# PDを可視化
fs = [lambda x: x + 1 / 3, lambda x: x ** 2 + 0.5]
pd.plot(fs=fs, ylabel="Partial Dependence", title="理論的な関係とPDで推定された関係の比較（特徴量が強く相関）")

f:id:dropout009:20210808015752p:plain

このように、モデルがデータの存在しない範囲においてもうまく予測ができる場合は、たとえ特徴量に強い相関があってもPDで理論的な関係を復元することができます。
ただし、外挿がうまくいくという状況は、今回の例のように特定化に完璧に成功した線形回帰モデルなど、あまり現実的でないことが多いです。
Random ForestやNeural Netなどのフレキシブルなモデルを利用すると外挿がうまくいかないことが多いので、特徴量が強く相関する場合はALEを使うことが無難と言えます。

参考文献

Apley, Daniel W., and Jingyu Zhu. "Visualizing the effects of predictor variables in black box supervised learning models." Journal of the Royal Statistical Society: Series B (Statistical Methodology) 82.4 (2020): 1059-1086.
Molnar, Christoph. "Interpretable machine learning. A Guide for Making Black Box Models Explainable." (2019). https://christophm.github.io/interpretable-ml-book/.
Limitations of Interpretable Machine Learning Methods: https://compstat-lmu.github.io/iml_methods_limitations/.
森下光之助. 「機械学習を解釈する技術〜予測力と説明力を両立する実践テクニック」. 技術評論社. (2021).

2021-07-31

因果推論とOLS：OLS推定量は何を推定しているのか（Słoczyński, 2020）

OLS Python 回帰分析シミュレーション因果推論

$\def\paren#1{\left(#1\right)} \def\brac#1{\left[#1\right]} \def\P#1{\Pr\paren{#1}} \def\E#1{\mathbb{E}\brac{#1}} \def\var#1{\mathrm{Var}\brac{#1}} \def\ate{\mathrm{ATE}} \def\att{\mathrm{ATT}} \def\atu{\mathrm{ATU}}$

はじめに
OLS推定量は何を推定しているのか
シミュレーション
OLS推定量の理論値の確認
まとめ
参考文献

はじめに

こちらの@yohei_econさんのツイートを見て知ったのですが、OLS推定量が一体何を推定しているのかを因果推論の文脈で改めて考え直す論文が発表されていました。

自分の不勉強をさらしますが、selection biasをコントロールできていれば、OLSではATTを推定できると思っていたのですが、違うかな？

去年出たこのREStatの論文をみると、OLSの推定量はATTとATUの凸結合で、treatedの割合が増えると、推定値はむしろATUに近づくいう結論。https://t.co/agfcIZGz0z
— 小林庸平 | Yohei KOBAYASHI (@yohei_econ) 2021年7月12日

この記事では、Słoczyński(2020) "Interpreting ols estimands when treatment effects are heterogeneous: Smaller groups get larger weights."の主張を紹介し、その主張が成り立っているのかをシミュレーションで確認します。

OLS推定量は何を推定しているのか

因果推論の文脈で処置効果（treatment effect）を推定する様々な手法が提案されていますが、実務家の中ではまだまだ線形回帰モデルを用いてOLSで処置効果を分析している例が多く見られます。
処置効果をOLSで推定する典型的な例として、以下のような線形回帰モデル

$\begin{align} Y = \alpha + \tau D + X'\beta + U \end{align}$

を考えます。
ここで、それぞれ

$Y$ ：目的変数
$D$ ：処置を受けたら1、受けていなければ0をとるダミー変数
$X$ ：コントロール変数
$U$ ：誤差項
$\tau$ ：OLSで推定される処置効果
$(\alpha, \beta)$ ：その他の回帰パラメータ

を表しています。

平たく言うと、「処置変数 $D$ とコントロール変数 $X$ をぜんぶ回帰モデルに突っ込んで、処置変数 $D$ の回帰係数 $\tau$ を推定したら、これが処置の平均的な効果でしょ」というのがこのモデルの発想です。
実際、処置効果が $\tau$ で一定なら、OLSで推定した処置効果は（いくつかの仮定のもとで）真の処置効果と一致します。
問題は、 $\tau(X)$ のように処置効果に異質性がある場合、つまり、処置を受けるユニットの属性によって処置効果が異なる場合です。
例えば、個人に対する処置効果を考えると、性別や年齢によって効果が異なるというのはありそうな話です。

処置効果が属性によって異なり、さらに処置を受けたグループと受けていないグループで属性が異なるような状況を考えます。
このとき、よく利用されるestimand（推定したい効果）として

ATE：サンプル全体に対する平均的な処置効果
ATT：処置群に対する平均的な処置効果
ATU：対照群に対する平均的な処置効果

が挙げられます。
それぞれ、サンプル全体、処置群、対照群に対する平均的な効果を推定しています。
ここで、（処置効果の異質性を明示的に考慮せずに）線形回帰モデル $Y = \alpha + \tau D + X'\beta + U$ で処置効果 $\tau$ を推定した場合、一体どのグループに対する平均的な処置効果が推定されるのでしょうか？
この疑問に対して、OLSで推定された処置効果は（いくつかの仮定のもとで）以下のようなATTとATUの加重平均になるというのが論文の主張です。

$\begin{align} \tau = w\tau_{\att} + (1-w)\tau_{\atu} \end{align}$

ここで、重み $w$ は

\begin{align}
w &= \frac{\paren{1 - \rho}\var{e(X) \mid D=0}}{\rho\var{e(X) \mid D=1} + \paren{1 - \rho}\var{e(X) \mid D=0}}
\end{align}

で定義され、 $\rho = \P{D=1}$ はサンプルに占める処置群の割合を、さらに $e(X) = \P{D = 1 \mid X}$ は処置を受ける確率を表します。

話を簡単にするために、いったん処置を受ける確率の条件付き分散は一定（ $\var{e(X) \mid D=0} = \var{e(X) \mid D=1} = \sigma^2$ ）としましょう。
すると、重み $w$ は

$\begin{align} w &= \frac{\paren{1 - \rho}\sigma^2}{\rho\sigma^2 + \paren{1 - \rho}\sigma^2}\\ &= 1 - \rho \end{align}$

と簡略化できます。
よって、OLSで推定した処置効果は、

$\begin{align} \tau = \paren{1-\rho}\tau_{\att} + \rho\tau_{\atu} \end{align}$

と書けます。
つまり、サンプルに占める処置群の割合が大きくなるほどATUに近くなり、対照群の割合が大きくなるほどATTに近くなることがわかります。

OLSで推定した処置効果はATTとATUの加重平均なのでATEになっているかというと、そうでもありません。
ATEはサンプル全体の処置効果なので、ATTは処置群の割合で、ATUは対照群の割合で重みを付けて加重平均します。

$\tau_{\ate} = \rho \tau_{\att} + \paren{1-\rho}\tau_{\atu}$

つまり、OLSによって推定される処置効果は、ATEとは逆の割合でATTとATUの重みを付けた加重平均になっていると言えます。

シミュレーション

それでは、処置効果に異質性がある場合のOLS推定量の振る舞いをシミュレーションで確認してみましょう。
以下の設定でシミュレーションデータを生成します（あんまり設定に自信がないのでおかしかったら教えて下さい）。

$\begin{align} Y &= \tau(X) D + X + U,\\ X &\sim \mathrm{Uniform}(0, 1),\\ D &\sim \mathrm{Bernoulli}(e(X)),\\ U &\sim \mathcal{N}(0, 0.1^2),\\ \tau(X) &= X,\\ e(X) &= \P{D = 1 \mid X} = \theta X\\ \theta &\in (0, 1] \end{align}$

ここで、

説明変数 $X$ は区間 $[0, 1$ ]の一様分布から生成します。 $X$ は目的変数 $Y$ 、 $D=1$ になる確率 $e(X)$ 、処置効果の強さ $\tau(X)$ の3つに影響を与えます
処置変数 $D$ は成功確率 $e(X)$ のベルヌーイ分布から生成します
ノイズ $U$ は平均0、分散0.01の正規分布から生成します
処置効果 $\tau(X) = X$ としています。つまり、処置効果には異質性があり、 $X$ が大きいユニットほど処置効果 $\tau(X)$ が大きくなります
処置変数 $D$ が1になる確率は $e(X) = \P{D = 1 \mid X} = \theta X$ としています。つまり、 $X$ が大きいユニットほど処置を受ける確率が高くなります。なお、 $X$ は目的変数 $Y$ にも直接影響を与えるので、いわゆる交絡が発生しています
$\theta$ は0より大きく1以下の値をとるパラメータで、 $\theta$ が大きいほど処置群の割合が大きくなります

それでは、この設定でシミュレーションデータを生成し、OLSによる処置効果 $\tau$ を推定します。
合わせて、ATE、ATT、ATU、処置群の割合 $\rho$ 、重み $w$ などの各種理論値を計算し、OLS推定量と各種指標の関係を確認します。

# 関数を用意
def generate_simulation_data(
    n_samples: int, theta: float
) -> tuple[np.ndarray, np.ndarray, np.ndarray, np.ndarray]:
    """シミュレーションデータの生成"""

    X = np.random.uniform(0, 1, n_samples)
    U = np.random.normal(0, 0.1, n_samples)

    e_X = theta * X
    D = np.random.binomial(1, e_X, n_samples)
    tau = X

    Y = tau * D + X + U

    return (X, Y, D, tau, e_X)


def estimate_tau(X: np.ndarray, D: np.ndarray, Y: np.ndarray) -> float:
    """OLSによる処置効果tauの推定"""

    Z = np.column_stack([X, D])

    return (np.linalg.inv(Z.T @ Z) @ (Z.T @ Y))[1]


def calc_treatment_effect(
    D: np.ndarray, tau: np.ndarray, e_X: np.ndarray
) -> tuple[float, float, float, float, float]:
    """理論上の各種処置効果を計算"""
    
    is_treat = D.astype(bool)

    att = tau[is_treat].mean()
    atu = tau[~is_treat].mean()
    ate = tau.mean()

    rho = D.mean()
    var_e_0 = tau[~is_treat].var()
    var_e_1 = tau[is_treat].var()
    w = (1 - rho) * var_e_0 / ((1 - rho) * var_e_0 + rho * var_e_1)

    return (att, atu, ate, rho, w)


# thetaの値を変動させたときにOLSを推定量tauがどのように変化するかをシミュレーション
thetas = np.arange(0.1, 1.1, 0.1)

# thetaの数 x (rho, w, ols, att, atu, ate)
results = np.zeros((thetas.shape[0], 6))

for t, theta in enumerate(thetas):
    # データを生成
    X, Y, D, tau, e_X = generate_simulation_data(n_samples=1000000, theta=theta)
    
    # 処置効果tauをOLSで推定
    tau_hat = estimate_tau(X, D, Y)
    
    # 処置効果の理論値を計算
    att, atu, ate, rho, w = calc_treatment_effect(D, tau, e_X)
    
    # 各種指標を保存
    results[t, :] = np.array([rho, w, tau_hat, att, atu, ate])

シミュレーション結果をデータフレームにまとめて確認します。

# 結果をデータフレームとしてまとめる
df_simulation = pd.DataFrame({"theta": thetas})
df_simulation[["rho", "w", "OLS", "ATT", "ATU", "ATE"]] = results

df_simulation

	theta	rho	w	OLS	ATT	ATU	ATE
0	0.1	0.050065	0.966249	0.660375	0.666286	0.491588	0.500334
1	0.2	0.100121	0.930907	0.653444	0.666652	0.481084	0.499663
2	0.3	0.149789	0.894566	0.646695	0.667451	0.470407	0.499922
3	0.4	0.199862	0.854556	0.636324	0.666510	0.458109	0.499760
4	0.5	0.250508	0.811860	0.624971	0.666640	0.444622	0.500239
5	0.6	0.300161	0.766195	0.610725	0.666141	0.428775	0.500023
6	0.7	0.349942	0.716122	0.594028	0.666906	0.411010	0.500559
7	0.8	0.399781	0.657424	0.572534	0.667729	0.388805	0.500313
8	0.9	0.449101	0.587984	0.542068	0.666661	0.363010	0.499380
9	1.0	0.499524	0.499813	0.499930	0.666453	0.332371	0.499253

データフレームだけだと分かりづらいので結果を可視化しておきます。

def draw_line(df: pd.Dataframe, title: str) -> None:
    """シミュレーション結果を可視化"""

    df_to_draw = df.melt(
        id_vars=["theta", "rho", "w"],
        value_vars=["OLS", "ATT", "ATE", "ATU"],
        var_name="kind",
    )

    fig, ax = plt.subplots()
    sns.lineplot("rho", "value", hue="kind", data=df_to_draw, ax=ax)
    fig.suptitle(title)
    fig.savefig(f"output/{title}")
    fig.show()


# 可視化
draw_line(df_simulation, "シミュレーション結果の可視化")

f:id:dropout009:20210727212712p:plain

まず、処置効果は $\tau(X) = X$ で、 $X$ は区間 $[0, 1$ ]の一様分布に従うので、ATEは処置群の割合 $\rho$ によらず常に0.5です。
ATTも処置群に割合によらず $0.66$ で固定されているようにみえます。
これはATEほど明らかでないので、後ほど理論的な値を確認します。
また、ATUは処置群の割合が増えるほど小さくなっていきます。

さて、今回興味があるのはOLSによる処置効果の推定です。
グラフを確認すると、 $\theta$ が小さく結果として処置群の割合 $\rho$ が小さいときは、ATTと近い値をとっています。
一方で、処置群の割合 $\rho$ が大きくなっていくにつれて、OLS推定量はATTから離れてATUに近づいていく様子が見て取れます。
最終的に $\rho = 0.5$ のときは、ATTとATUのちょうど中間に値になっています。
これは論文で主張している理論的なふるまいと一致しており、論文の主張をシミュレーションで確かめることができたと言えるでしょう。

OLS推定量の理論値の確認

シミュレーション結果でATTが一定であるなどの結果になりましたが、正直あんまり直感的でなくて不安なので理論的な数値も確認しておきました。
まず、 $X$ が区間 $[0, 1$ ]の一様分布に従うことを利用するとATEはすぐに計算できます。

$\begin{align} \tau_{\ate} &= \E{\tau(X)} = \E{X} = \frac{1}{2} \end{align}$

ATTはちょっと面倒ですが、ベイズの定理で変換することで計算できます。

$\begin{align} \tau_{\att} &= \E{\tau(X) \mid D = 1} \\ &= \int \tau(x) p(x \mid D=1) dx\\ &= \int \tau(x)\frac{\P{D = 1 \mid X = x}p(x) }{\P{D=1}}dx \end{align}$

ここで、それぞれのパーツは

$\begin{align} \tau(x) &= x,\\ \P{D = 1 \mid X = x} &= \theta x,\\ p(x) &= 1, \\ \P{D=1} &= \E{\P{D = 1 \mid X = x}}, \\ &= \E{\theta X} \\ &= \theta \E{X} \\ &= \frac{1}{2}\theta \end{align}$

なので、これらを元の式に代入するとATTを得ます。

$\begin{align} \tau_{\att} &= \int_0^1 x\frac{\theta x }{\theta / 2}dx\\ &= 2\int_0^1 x^2dx\\ &= \frac{2}{3} \end{align}$

同様にATUも計算します。対照群に対する処置効果を計算するので、

\begin{align}
\P{D = 0 \mid X = x} &= 1 - \theta x\\
\P{D=1} &= 1 - \frac{1}{2}\theta
\end{align}

に注意しながらATTと同様にベイズの定理を用いると

$\begin{align} \tau_{\atu} &= \E{\tau(X) \mid D = 0} \\ &= \int \tau(x) p(x \mid D=1) dx\\ &= \int \tau(x)\frac{\P{D = 0 \mid X = x}p(x) }{\P{D=0}}dx\\ & = \int_0^1 x\frac{1 - \theta x }{1 - \theta / 2}dx\\ &= \frac{2- 3\theta}{3(2 - \theta)} \end{align}$

となります。

最後に重み $w$ つまり

\begin{align}
w &= \frac{\paren{1 - \rho}\var{e(X) \mid D=0}}{\rho\var{e(X) \mid D=1} + \paren{1 - \rho}\var{e(X) \mid D=0}}
\end{align}

を計算します。

ひとつひとつのパーツをバラバラに計算して、最後にまとめます。
まずは $D=1$ で条件づけた処置を受ける確率の条件付き分散は

\begin{align}
\var{e(X) \mid D = 1}
&=\E{e(X)^2 \mid D = 1} - \E{e(X) \mid D = 1}^2
\end{align}

なので、

\begin{align}
\E{e(X) \mid D = 1} &= \int e(x)p(x \mid D = 1) = 2\theta\int_0^1 x^2 dx = \frac{2}{3}\theta,\\
\E{e(X)^2 \mid D = 1} &= \int e(x)^2p(x \mid D = 1) = 2\theta^2\int_0^1 x^3 dx = \frac{1}{2}\theta^2
\end{align}

であることを利用すると

\begin{align}
\var{e(X) \mid D = 1}
&= \paren{\frac{1}{2}\theta^2} - \paren{\frac{2}{3}\theta}^2\\
&= \frac{1}{18}\theta^2
\end{align}

となることがわかります。

同様にして、 $D=0$ で条件づけた処置を受ける確率の条件付き分散は

\begin{align}
\var{e(X) \mid D = 0}
&=\E{e(X)^2 \mid D = 0} - \E{e(X) \mid D = 0}^2
\end{align}

なので、

\begin{align}
\E{e(X) \mid D = 0} &= \int e(x)p(x \mid D = 0) = \frac{2\theta}{2 - \theta}\int_0^1 \paren{x - \theta x^2} dx = \frac{\theta(3 - 2\theta)}{3(2 - \theta)},\\
\E{e(X)^2 \mid D = 0} &= \int e(x)^2p(x \mid D = 0) = \frac{2\theta^2}{2 - \theta}\int_0^1 \paren{x^2 - \theta x^3} dx = \frac{\theta^2(4 - 3\theta)}{6(2-\theta)}
\end{align}

であることを考慮すると

\begin{align}
\var{e(X) \mid D = 0}
&= \paren{\frac{\theta^2(4 - 3\theta)}{6(2-\theta)}} - \paren{\frac{\theta(3 - 2\theta)}{3(2 - \theta)}}^2\\
&= \frac{\theta^2\paren{\theta^2 - 6\theta + 6}}{18 \paren{2 - \theta}^2}
\end{align}

となります。
ここから重み $w$ を計算することができます。

理論値の計算方法がわかったので、これらの理論値を計算する関数を用意して、可視化します。

def calc_theoretical_value(theta: np.ndarray) -> pd.DataFrame:

    ate = 0.5
    att = 2 / 3
    atu = (3 - 2 * theta) / (3 * (2 - theta))
    rho = 0.5 * theta

    var_e_0 = theta ** 2 * (theta ** 2 - 6 * theta + 6) / 18 / (2 - theta) ** 2
    var_e_1 = theta ** 2 / 18
    w = (1 - rho) * var_e_0 / ((1 - rho) * var_e_0 + rho * var_e_1)
    ols = w * att + (1 - w) * atu

    df = pd.DataFrame(
        {
            "theta": theta,
            "rho": rho,
            "w": w,
            "OLS": ols,
            "ATT": att,
            "ATU": atu,
            "ATE": ate,
        }
    )
    return df


# 理論値を計算
df_theory = calc_theoretical_value(theta=np.arange(0.1, 1.05, 0.1))

# 可視化
draw_line(df_theory, "理論値を可視化")

f:id:dropout009:20210727212719p:plain

理論値はシミュレーション結果と整合的であることが見て取れます。
よかった！

まとめ

この記事では、Słoczyński(2020)の主張を紹介し、実際にその主張が成り立っているのかをシミュレーションで確認しました。
処置効果に異質性がある場合、OLS推定量はサンプルに占める処置群の割合が大きくなるほどATUに近くなり、対照群の割合が大きくなるほどATTに近くなることがわかりました。

線形回帰モデルが一体何を推定しているかを因果推論の文脈で改めて考える取り組みはすごく面白いトピックだと思っていて、まだまだ勉強していきたいです。

参考文献

Słoczyński, Tymon. "Interpreting ols estimands when treatment effects are heterogeneous: Smaller groups get larger weights." The Review of Economics and Statistics (2020): 1-27.

2021-07-26

バイアス-バリアンスの分解と、アンサンブルの話

機械学習シミュレーション Python 統計学 ensemble bias variance scikit-learn

$\def\calD{\mathcal{D}} \def\paren#1{\left(#1\right)} \def\brac#1{\left[#1\right]} \def\quad#1{\paren{#1}^2} \def\sumi{\sum_{i=1}^N} \def\sumk{\sum_{k=1}^K} \def\E#1{\mathbb{E}_{\calD}\brac{#1}} \def\var#1{\mathrm{Var}_{\calD}\brac{#1}} \def\cov#1{\mathrm{Cov}_{\calD}\brac{#1}} \def\bias#1{\mathrm{Bias}_{\calD}\brac{#1}} \def\hf{\hat{f}_{\calD}} \def\hfk{\hf^k} \def\fx{f(x^*)} \def\hfx{\hf(x^*)} \def\hfkx{\hfk(x^*)} \def\Ehfx{\E{\hfx}} \def\Ehfkx{\E{\hfkx}} \def\mse{\mathrm{MSE}_{\calD}} \def\ss{\sigma^2_*} \def\cc{\sigma_{**}}$

はじめに
バイアスとバリアンスの分解
シミュレーションでバイアスとバリアンスの関係を確認する
モデルのアンサンブルでばらつきを抑える
- アンサンブルの効果を数式で確認する
  - バイアス
  - バリアンス
- アンサンブルの効果をシミュレーションで確認する
まとめ
参考文献

はじめに

この記事では、バイアス（偏り）とバリアンス（分散、ばらつき）の分解について、数式とシミュレーションの両面から確認し、

ある種の予測誤差はモデルのバイアスとバリアンスに分解できること
バイアスとバリアンスにはトレードオフの関係があること
モデルのアンサンブルはバリアンスの減少を通じて予測精度を改善できること
アンサンブルはモデル同士の相関が小さいほど有効なこと

を示します。

バイアスとバリアンスの分解

バイアスとバリアンスの分解を考えるため、まずは数式を用いた定式化を行います。

$J$ 個の説明変数を $X = (X_1, \dots, X_J)$ 、目的変数を $Y$ とします。
真の関数形は $f(x)$ で、目的変数はこれにノイズ $U$ が乗って観測されるとします。

\begin{align}
Y_i = f(X_i) + U_i
\end{align}

$N$ 個の観測されたデータの組を $\calD = \{(X_i, Y_i)\}_{i=1}^N$ とします。
適当なアルゴリズムを使って、データ $\calD$ を学習して予測モデル $\hf(x)$ を構築します。
得られた予測モデルを用いて新しいデータ $x^*$ に対する予測を行います。
真の値 $\fx$ と比べてこの予測値 $\hfx$ がどのくらいずれるのかがこの記事の興味の対象になります。

予測誤差は二乗誤差で評価することにします。
観測データはサンプリングされたものなので、データ $\calD$ のばらつき応じて学習済みモデルも変動し、予測値も変わるはずです。
そこで、二乗誤差の期待値をとることにし、これを平均二乗誤差（MSE)と呼ぶことにします。
このとき、新しいデータ $x^*$ に対するMSEは以下で表現できます。

\begin{align}
\mse(x^*) = \E{\quad{\fx - \hfx}}
\end{align}

ここで、何に対して期待値をとっているかを明示的にするため $\E{\cdot}$ という表記を用いています。

実は、MSEはモデルの偏り（バイアス）とモデルの安定性（バリアンス）に分解できることが知られています。
バイアスとバリアンスの正確な定義は後ほど触れます。
まず、 $\Ehfx$ を足して引くことでMSEを3つのパートに分解できます。

\begin{align}
\mse(x^*)
=& \E{\quad{\fx - \Ehfx - \paren{\hfx - \Ehfx}}}\\
=& \E{\quad{\fx - \Ehfx}} \\
&- \E{2\paren{\fx - \Ehfx}\paren{\hfx - \Ehfx}} \\
&+ \E{\quad{\hfx - \Ehfx}}
\end{align}

ここで、 $\fx$ とか $\Ehfx$ は確率変数ではなく確定的な値なので期待値の外に出せます。

\begin{align}
\mse(x^*)
=& \quad{\fx - \Ehfx} \\
&- 2\paren{\fx - \Ehfx}\paren{\Ehfx - \Ehfx} \\
&+ \E{\quad{\hfx - \Ehfx}}
\end{align}

第二項は0になるので、残りは第一項と第三項です。
これらはそれぞれバイアスとバリアンスと呼ばれています。

\begin{align}
\bias{\hfx} &= \fx - \Ehfx, \\
\var{\hfx} &= \E{\quad{\hfx - \Ehfx}}
\end{align}

バリアンスはモデルの予測値 $\Ehfx$ が訓練データの影響を受けてどのくらいばらつくのかを表す指標です。
僕たちが観測するデータは母集団からのサンプリングなので、仮想的に何度もサンプリングを行うと毎回少し違うデータが観測されるわけですが、そのデータが少し違うことに対してどのくらい予測値が安定的かがバリアンスに反映されます。
ちょっと違うデータが与えられたときにモデルの予測が大きく異なるならバリアンスは大きく、逆にデータが変動しても似たような予測値を返すならバリアンスは小さくなります。

一方で、バイアスはモデルの予測の期待値 $\Ehfx$ が、真の値 $\fx$ からどのくらいずれるのかを表す指標です。
ここで、あくまで期待値の意味でのずれに焦点があたっていることに注意してください。
例えば、バリアンスの大きいモデルは、仮想的に何度もサンプリングを行う状況を考えると毎回違う予測値を出しますが、それを平均すると真の値 $\fx$ と近くなっているのか？ということをバイアスは測定していると解釈できます。

元の式に戻ると、MSEはバイアス（の二乗）とバリアンスに分解できることがわかります。

\begin{align}
\mse(x^*) = \bias{\hfx}^2 + \var{\hfx}
\end{align}

この分解はバイアス-バリアンス分解（bias-variance decomposition）と呼ばれています。

一般に、モデルが単純な場合はバリアンスが小さい代わりにバイアスが大きくなります。
一方で、モデルが複雑な場合はバイアスが小さい代わりにバイアスが大きくなります。
このように、バイアスとバリアンスにはトレードオフが存在し、これはbias-variance tradeoffと呼ばれています。
MSEはバイアスとバリアンスの足し算で決まるので、バイアスとバリアンスがいい塩梅になるようにモデルの複雑さを決めることが予測精度の高いモデルを構築する際には重要です。

なお、上記で計算したMSEはある入力 $x^*$ に対するものなので、もし平均的な予測誤差を知りたい場合は

\begin{align}
\mathbb{E}_{X^*}\brac{{\mse(X^*)}}
\end{align}

のように入力の確率分布を用いて期待値をとる必要があることに注意してください。

シミュレーションでバイアスとバリアンスの関係を確認する

シミュレーションの設定

以下の設定でシミュレーションデータを生成します。

\begin{align}
Y &= \sin(6 \pi X) + U,\\
X &\sim \mathrm{Uniform}(0, 1),\\
U &\sim \mathcal{N}(0, 1)
\end{align}

ここで、説明変数 $X$ は区間 $[0, 1$ ]の一様分布から生成します。
$X$ にsin関数を噛ませて、ノイズ $U$ を乗せて目的変数としています。
ノイズ $U$ は平均0、分散1の正規分布から生成します。

この設定で、データを生成してモデルを学習し予測する、ということを何回も繰り返して、モデルのバイアスとバリアンスを確認することにします。
シミュレーションを行いその結果を可視化するために以下のSimulatorクラスを実装しました。

@dataclass
class Simulator:
    """シミュレーションとその結果の可視化を行うクラス

    Args:
        n_grids: Xの理論値をどのくらい細かく作成するか
    """

    n_grids: int = 100

    def __post_init__(self) -> None:
        """理論値を作成"""

        # シミュレーションの関数形を特定
        self.f = lambda X: np.sin(6 * np.pi * X)

        # Xの範囲をグリッドで分割
        self.X_theory = np.linspace(start=0, stop=1, num=self.n_grids)

        # f(X)で理論値を作成
        self.y_theory = self.f(self.X_theory)

    def generate_simulation_data(
        self, n_instances: int
    ) -> tuple[np.ndarray, np.ndarray]:
        """シミュレーション用のデータを生成する

        Args:
            n_instances: シミュレーションで生成するインスタンスの数
        Returns:
            特徴量と目的変数のtuple
        """

        # Xは一様分布から、yは正規分布から生成する
        X = np.random.uniform(low=0, high=1, size=n_instances)
        u = np.random.normal(loc=0, scale=1, size=n_instances)
        # 関数f(X)を噛ませてノイズを足して目的変数とする
        y = self.f(X) + u

        return (X, y)

    def simulate(
        self, estimators: dict[str, Any], n_simulations: int, n_instances: int
    ) -> dict[str, np.ndarray]:
        """シミュレーションデータを生成して、学習と予測を行う

        Args:
            estimators: シミュレーション用のモデル
            n_simulations: シミュレーション回数
            n_instances: シミュレーションで生成するインスタンスの数
        Returns:
            モデルごとの予測値がまとまった辞書
        """

        y_preds = {
            k: np.zeros((self.n_grids, n_simulations)) for k in estimators.keys()
        }
        for s in range(n_simulations):
            X, y = self.generate_simulation_data(n_instances)
            for k, estimator in estimators.items():
                y_preds[k][:, s] = estimator.fit(X.reshape(-1, 1), y).predict(
                    self.X_theory.reshape(-1, 1)
                )

        return y_preds

    def decompose_bias_variance(
        self,
        y_preds: dict[str, np.ndarray],
    ) -> dict[dtr, dict[str, np.ndarray]]:
        """バイアスとバリアンスに分解する

        Args:
            y_preds: モデルごとの予測値
        Returns:
            BiasとVarianceがまとまった辞書
        """

        bias = {
            k: (self.y_theory - y_pred.mean(axis=1)) ** 2
            for k, y_pred in y_preds.items()
        }
        variance = {k: y_pred.var(axis=1) for k, y_pred in y_preds.items()}

        return {"Bias2": bias, "Variance": variance}

    def draw_prediction(
        self,
        y_preds: dict[str, np.ndarray],
        estimator_key: int,
        simulation_ids: list[int],
        ylim: tuple(float, float) | None = None,
    ) -> None:
        """予測結果を可視化

        Args:
            y_preds: 予測結果
            estimator_key: 可視化したいモデルの名前
            simulation_ids: 何回目のシミュレーション結果を可視化するか
            ylim: グラフの上限下限を調整したいときに使う
        """

        if ylim is None:
            y = np.concatenate([y for y in y_preds.values()])
            ylim = (y.min(), y.max())

        fig, axes = plt.subplots(ncols=2, figsize=(8, 4))

        # バイアスの可視化
        axes[0].plot(
            self.X_theory,
            y_preds[estimator_key].mean(axis=1),
            linewidth=2,
            label=f"予測値（シミュレーションの平均）",
        )
        axes[0].plot(self.X_theory, self.y_theory, color=".3", linewidth=2, label="理論値")
        axes[0].legend()
        axes[0].set(xlabel="X", ylabel="Y", ylim=ylim, title="Biasの可視化")

        # バリアンスの可視化
        axes[1].plot(self.X_theory, self.y_theory, color=".3", linewidth=2, label="理論値")

        for s in simulation_ids:
            axes[1].plot(
                self.X_theory,
                y_preds[estimator_key][:, s],
                linewidth=0.1,
                color=sns.color_palette()[0],
                label=f"予測値（シミュレーション{s:02.0f}）",
            )
        axes[1].set(xlabel="X", ylabel="Y", ylim=ylim, title="Varianceの可視化")

        fig.suptitle(f"{estimator_key}のBiasとVarianceを可視化")
        fig.savefig(f"output/{estimator_key}のBiasとVarianceを可視化")
        fig.show()

    def draw_bias_variance(
        self, bias_variances: dict[str, dict[str, np.ndarray]], title: str
    ) -> None:
        """バイアスとバリアンスを可視化する

        Args:
            bias_variances: decompose_bias_variance()の結果
        """

        fig, axes = plt.subplots(ncols=2, figsize=(8, 4))
        for ax, (k, bvs) in zip(axes, bias_variances.items()):
            for estimator_key, value in bvs.items():
                # Xは一様分布に従うので単に平均をとればいい
                avg = value.mean()
                ax.plot(
                    self.X_theory,
                    value,
                    linewidth=1,
                    label=f"{estimator_key}(AVG:{avg: .2f})",
                )
                ax.legend()
                ax.set(xlabel="X", title=k)
        fig.suptitle(title)
        fig.savefig(f"output/{title}")
        fig.show()

シミュレーション結果の確認

予測モデルとしては取り扱いの簡単さを重視して決定木を採用することにします。
ハイパーパラメータmax_depthを調整することでモデルの複雑さを簡単に制御することができます。

max_depthは決定木の最大分割回数を制御するハイパーパラメータで、例えば、max_depth=1なら決定木は一度しか分割を行わないので、2種類の予測値しか出しません。
この場合、モデルが非常に単純なので、バイアスが大きくバリアンスが小さくなることが予測されます。
一方で、max_depth=10なら最大で2の10乗つまり1024種類の予測値を出せることになります。
この場合はmax_depth=1よりもモデルが複雑になるので、バイアスが小さくバリアンスが大きくなるでしょう。

それでは、実際にmax_depth=1とmax_depth=10の決定木でシミュレーションを行います。
シミュレーションの回数は100回、一回のシミュレーションで生成するインスタンスの数は1000とします。

# シミュレーターインスタンスの作成
simulator = Simulator()

# 単純なモデルと複雑なモデルを用意
dts = {
    "DecisionTree(01)": DecisionTreeRegressor(max_depth=1),
    "DecisionTree(10)": DecisionTreeRegressor(max_depth=10),
}

# 予測結果
y_preds = simulator.simulate(estimators=dts, n_simulations=100, n_instances=1000)

# バイアスとバリアンスに分解
bias_variances = simulator.decompose_bias_variance(y_preds)

まずは、単純なmax_depth=1の場合を確認します。
モデルはsin関数の波をまともに捉えられておらず、バイアスが大きいことがわかります。
一方で、どのシミュレーションでも左端で分割するか右端で分割するかの2択がばらついているだけでほぼ同じような予測を行っており、バリアンスは小さいことが見て取れます。

# 単純なモデルの予測結果を可視化
# シミュレーション結果をすべて可視化するとうるさいので20個にしぼる
simulator.draw_prediction(
    y_preds=y_preds, simulation_ids=range(20), estimator_key="DecisionTree(01)"
)

f:id:dropout009:20210726192759p:plain

次に、複雑なmax_depth=10の場合を確認します。
モデルは（平均的には）sin関数の波を十分に捉えることができており、バイアスが小さいことがわかります。
一方で、シミュレーションごとに予測値はかなり荒れており、バリアンスは大きいことが見て取れます。

# 複雑なモデルの予測結果を可視化
simulator.draw_prediction(
    y_preds=y_preds, simulation_ids=range(20), estimator_key="DecisionTree(10)"
)

f:id:dropout009:20210726192803p:plain

モデルごとにバイアス（の二乗）とバリアンスを直接比較したグラフが下図になります。
単純なmax_depth=1のモデルはバイアスが大きい反面バリアンスが小さく、複雑なmax_depth=10のモデルはバイアスが小さい反面バリアンスが大きいことが見て取れます。
このように、シミュレーション結果はモデルのバイアスとバリアンスにはトレードオフがあることを示唆しています。

# モデルごとのバイアスとバリアンスを比較
simulator.draw_bias_variance(bias_variances=bias_variances, title="モデルごとのBias-Varianceの比較")

f:id:dropout009:20210726192806p:plain

バイアスとバリアンスのトレードオフを可視化する

単純なモデルと複雑なモデルにはバイアスとバリアンスのトレードオフがあることが示唆されました。
このトレードオフをより詳細に確認するため、max_depthを1から10まで変化させた際にバイアスとバリアンスがどのように変化するかを追跡しましょう。

# max_depthを1から10まで変化させる
max_depth_range = list(range(1, 11))
dts = {f'DT({x:02})': DecisionTreeRegressor(max_depth=x) for x in max_depth_range}

# 予測値を作成
y_preds = simulator.simulate(estimators=dts, n_simulations=100, n_instances=1000)

# バイアスとバリアンスを分解
bias_variances = simulator.decompose_bias_variance(y_preds)

def draw_bias_variance_tradeoff(
    bias_variances: dict[str, dict[str, np.ndarray]], max_depth_range: list
) -> None:
    """max_depthを変化させた際のバイアスとバリアンスの可視化"""

    bias = np.array([v.mean() for v in bias_variances["Bias2"].values()])
    variance = np.array([v.mean() for v in bias_variances["Variance"].values()])
    mse = bias + variance

    fig, ax = plt.subplots()
    ax.plot(max_depth_range, bias, label="Bias2")
    ax.plot(max_depth_range, variance, label="Variance")
    ax.plot(max_depth_range, mse, label="MSE")
    ax.legend()
    ax.set_xticks(max_depth_range)
    ax.set(xlabel="max_depth", ylabel="Bias/Variance/MSE")
    fig.suptitle("Bias-Varianceのトレードオフ")
    fig.savefig("Bias-Varianceのトレードオフ")
    fig.show()


draw_bias_variance_tradeoff(bias_variances, max_depth_range)

f:id:dropout009:20210726192948p:plain

モデルを複雑にするつれてバイアスが小さくなる反面バリアンスが大きくなっていく様子が見て取れます。
また、MSEはバイアスの二乗とバリアンスの足し算なので、最も理論値との誤差が小さくなるいい塩梅のハイパーパラメータはmax_depth=5であることがわかります。

モデルのアンサンブルでばらつきを抑える

ここまで、バイアスとバリアンスにはトレードオフがあることを見てきました。
モデルを複雑にすればバイアスは小さく出来ますが、代わりにバリアンスが大きくなってしまいます。
実は、バイアスを変化させずにバリアンスを小さくし得る手法として、モデルのアンサンブルが知られています。

アンサンブルの効果を数式で確認する

$K$ 個のベースになる予測モデル $\paren{\hf^1(x), \dots, \hf^K(x)}$ をアンサンブルして予測を行うことを考えます。
一番単純なアンサンブルとして、ベースモデルの単純平均を考えることにします。

\begin{align}
\hfx = \frac{1}{K}\sumk\hfk(x)
\end{align}

バイアス

予測モデルのアンサンブルはバイアスとバリアンスにどのような影響を与えるでしょうか？
まずはモデルのバイアスについて考えます。
バイアスの計算式に上式を代入して変形します。

\begin{align}
\bias{\hfx}
&= \fx - \Ehfx\\
&= \fx - \frac{1}{K}\sumk\hfkx\\
&= \frac{1}{K}\sumk\paren{\fx - \hfkx}\\
&= \frac{1}{K}\sumk\bias{\hfkx}\\
\end{align}

ここから、アンサンブルモデルの予測値のバイアスは各ベースモデルのバイアスの平均になることがわかります。
話を簡単にするために、ベースモデルのバイアスがすべて同じく $\delta$ だとします。
実際、バギングのように単に復元抽出を繰り返して予測モデルを複数作成しその結果を単純平均するようなアルゴリズムでは、ベースモデルのバイアスは一定だと考えられます。
このとき、アンサンブルモデルのバイアスは

\begin{align}
\bias{\hfx} &= \frac{1}{K}\sumk \delta = \delta
\end{align}

となり、アンサンブルによってバイアスが小さくなるなどの改善は見られないことがわかります。

バリアンス

次に、モデルのバリアンスについて考えます。

$\begin{align} \var{\hfx} &= \var{\frac{1}{K}\sumk\hfkx}\\ &= \quad{\frac{1}{K}}\paren{\sumk\var{\hfkx} + \sum_{k\neq k'}\cov{\hfkx, \hf^{k'}(x^*)}} \end{align}$

話を簡単にするために、すべてのベースモデルに関して分散が $\ss$ 、共分散が $\cc$ で一定だとします。
実際、バギングだとベースモデルは学習データが異なる以外に差分はないので分散も共分散も一定になります。
このとき、アンサンブルモデルのバリアンスは

$\begin{align} \var{\hfx} &= \quad{\frac{1}{K}}\paren{\sumk\ss + \sum_{k\neq k'}\cc}\\ &= \quad{\frac{1}{K}}\paren{K\ss + K(K-1)\cc}\\ &= \paren{\frac{1}{K}}\ss + \paren{\frac{K-1}{K}}\cc \end{align}$

と単純化できます。

ひとつ極端な状況として、仮にベースモデル同士の相関が全く無ケースを考えます。
このとき $\cc = 0$ であり、アンサンブルモデルのバリアンスは

$\begin{align} \var{\hfx} &= \paren{\frac{1}{K}}\ss \end{align}$

になります。
よって、ベースモデルの数を増やせば増やすほどアンサンブルモデルのバリアンスは小さくなっていき、結果としてMSEつまり予測誤差も小さくなります。

実際は、ベースモデル同士は大なり小なり相関があるので、ここまで極端な状況は起きませんが、それでも相関が小さいほどアンサンブルモデルのバリアンスは小さくなりやすいことは事実です。
これがアンサンブルを行う際のベースモデルは互いに相関が小さい方がいいと言われる理由です。

まとめると、モデルのアンサンブルはバイアスには影響を与えませんが、バリアンスを小さくすることを通じて予測誤差を改善させる効果があると言えます。

アンサンブルの効果をシミュレーションで確認する

モデルのアンサンブルによるバリアンスの改善が数式から確認できたので、さらにシミュレーションでも改善効果を確認しておきます。
まずは、アンサンブルモデルとして、決定木をベースモデルとしてバギングの結果を返すBaggingTreeRegressorクラスを実装しておきます。

バギングのアルゴリズムは以下になります。

訓練データと同じインスタンス数だけデータを復元抽出する
復元抽出したデータを使ってベースモデルを学習し、保存しておく
これを任意の回数繰り返す
予測を行う際は、複数作成した学習済みベースモデルを用いて複数の予測を行い、結果を平均して最終的な予測値とする

復元抽出のたびに訓練データがちょっと変化するので、個々のベースモデルは似ているが少し異なる予測値を出すことが予想されます。
このような、互いに相関はするが完全に相関しているわけではない予測結果を平均することで、バリアンスを抑えることがバギングの狙いです。

@dataclass
class BaggingTreeRegressor:
    """
    決定木をベースモデルとしてBootstrap Aggregationを行う

    Args:
        n_estimators: いくつツリーを作成するか
        tree_params: ツリーに渡すハイパーパラメータ
    """

    n_estimators: int
    tree_params: dict

    def fit(self, X: np.ndarray, y: np.ndarray) -> BaggingRegressor:
        """データを復元抽出して学習"""

        # インスタンスの数
        n_instances = X.shape[0]

        # 復元抽出のためのIDを「インスタンスの数 x ベースモデルの数」だけ作成
        ids = np.random.choice(n_instances, size=(self.n_estimators, n_instances))

        # 復元抽出されたデータで個々のベースモデルを学習して保存
        self.estimators = []
        for e in range(self.n_estimators):
            self.estimators.append(
                DecisionTreeRegressor(**self.tree_params).fit(X[ids[e]], y[ids[e]])
            )

        return self

    def predict(self, X: np.ndarray) -> np.ndarray:
        """予測結果を平均して返す"""

        return np.column_stack([e.predict(X) for e in self.estimators]).mean(axis=1)

それでは、単純な決定木とそのバギングでバイアスとバリアンスがどのように異なるのかをシミュレーションします。
max_depthは先程のシミュレーションで最も予測誤差の小さくなる5を指定します。
また、バギングでは100本の決定木をアンサンブルすることにします。

# 決定木とそのバギングバージョンを用意
dts = {
    'DecisionTree(05)': DecisionTreeRegressor(max_depth=5),
    'BaggingTree': BaggingTreeRegressor(n_estimators=100, tree_params={'max_depth': 5}),
}

# 予測結果
y_preds = simulator.simulate(estimators=dts, n_simulations=100, n_instances=1000)

# バイアスとバリアンスの分解
bias_variances = simulator.decompose_bias_variance(y_preds)

決定木の予測結果をバギングの予測結果を比較すると、バイアスは同じようなものですがバギングはバリアンスがかなり抑えられていることが見て取れます。

# 決定木の予測結果を可視化
simulator.draw_prediction(y_preds=y_preds, simulation_ids=range(20), estimator_key='DecisionTree(05)')

f:id:dropout009:20210726192811p:plain

# バギングの予測結果を可視化
simulator.draw_prediction(y_preds=y_preds, simulation_ids=range(20), estimator_key='BaggingTree')

f:id:dropout009:20210726192817p:plain

実際、単純な決定木とバギングの結果を直接比較すると、バリアンスが三分の一程度に抑えられていることがわかります。
モデルのアンサンブルによるバリアンスの改善をシミュレーションからも確認することができました。

# 決定木とバギングでバイアスとバリアンスを比較
simulator.draw_bias_variance(bias_variances, title="決定木とバギングのBias-Varianceの比較")

f:id:dropout009:20210726192823p:plain

まとめ

この記事では、バイアスとバリアンスの分解について、理論とシミュレーションの両面から確認しました。

モデルの予測精度を表すMSEは、バイアスとバリアンスに分解できる
バイアスとバリアンスにはトレードオフがある。モデルが単純だとバイアスが大きいがバリアンスは小さく、モデルが複雑だとバイアスが小さいがバリアンスは大きい
モデルのアンサンブルはバリアンスを減少させることを通じて予測精度を改善することができる。モデル同士の相関が小さいほどアンサンブルの効果が高い

この記事で利用したシミュレーションコードは以下になります。

https://github.com/dropout009/bias_variance

参考文献

Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. The elements of statistical learning. Vol. 1. No. 10. New York: Springer series in statistics, 2001.

2021-07-23

多重共線性と回帰係数の信頼性の話。あとリッジ回帰。

Ridge regression シミュレーション回帰分析機械学習正則化統計学 Python

$\def\paren#1{\left(#1\right)} \def\brac#1{\left[#1\right]} \def\sumi{\sum_{i=1}^N} \def\P#1{\Pr\paren{#1}} \def\E#1{\mathbb{E}\brac{#1}} \def\var#1{\mathrm{Var}\brac{#1}} \def\hvar#1{\widehat{\mathrm{Var}}\brac{#1}} \def\quad#1{\paren{#1}^2} \def\inv#1{\paren{#1}^{-1}} \def\Xij{X_{i, j}} \def\vX{\mathbf{X}} \def\vXj{\mathbf{X}_j} \def\vXmj{\mathbf{X}_{\setminus j}} \def\vY{\mathbf{Y}} \def\vU{\mathbf{U}} \def\hvU{\hat{\vU}} \def\vVj{\mathbf{V}_j} \def\hvVj{\hat{\mathbf{V}}_j} \def\mM{\mathbf{M}} \def\mMj{\mathbf{M}_j} \def\mMmj{\mathbf{M}_{\setminus j}} \def\vP{\mathbf{P}} \def\mW{\mathbf{W}} \def\vI{\mathbf{I}} \def\hbeta{\hat{\beta}} \def\betamj{\beta_{\setminus j}} \def\hbetamj{\hbeta_{\setminus j}} \def\hgamma{\hat{\gamma}} \def\hXij{\hat{X}_{i, j}} \def\hVij{\hat{V}_{i, j}} \def\bXj{\bar{X}_{j}}$

はじめに
多重共線性とOLS推定量の信頼度
シミュレーションによる信頼度の確認
リッジ推定量で推定量の信頼性を高める
まとめ
参考文献

はじめに

先日、多重共線性に関する @hizakayuさんや@M123Takahashiさんのコメントを目にしました。

多重共線性の問題は，どの説明変数に強い相関があるかにより変わります．たとえば，y=b0+b1x1+b2x2+b3x3で，x1からyへの効果b1に興味があり，x2とx3は交絡因子とします．cor(x1,x2)>0.9は問題になり得ますが，cor(x2,x3)>0.9は気にする必要はありません．b2とb3の推定には興味がないからです．（続く） https://t.co/4d0gDukAB4
— 高橋将宜 Masayoshi Takahashi (@M123Takahashi) 2021年6月14日

【多重共線性と推定値の話】
昨日、これについて、教科書を紹介してもらい、勉強して少しまとめたので、Twitterの海に流します🌊 https://t.co/kDbySASiuj
— コムラ (@hizakayu) 2021年6月15日

恥ずかしながら、ここで紹介されている多重共線性と推定量の信頼性に関する性質のことは普通に忘れていました。
こちらのコメントを見てそういえばこんなこと習ったなと思い出し、大学院のころの資料*1や計量経済学の教科書*2を確認し、改めて学びなおしたことを記事としてまとめました。

この記事では、まずは多重共線性がある場合のOLS推定量の分散について数式を用いて確認します。
次に、数式で確認した結果をシミュレーションを用いて実際にみていきます。
最後に、推定量の信頼性を高める手法としてリッジ推定量を紹介し、リッジ推定量は（バイアスという犠牲を払うことで）信頼性を高められるを確認します。

多重共線性とOLS推定量の信頼度

線形回帰モデルの導入

以下のような線形回帰モデル

\begin{align}
Y_i = X_i'\beta + U_i
\end{align}

を考えます。ここで、 $Y_i$ は目的変数、 $X_i = (X_{i, 1}, \dots, X_{i, J})'$ は説明変数、 $U_i$ は誤差項を表します。
$i = 1, \dots, N$ はサンプルを表す添字で、 $\{X_i, Y_i\}_{i=1}^N$ はランダムサンプリングされているとします。
$\beta = (\beta_1, \dots, \beta_J)'$ は回帰係数です。

以下、表記を単純にするため行列を利用します。

\begin{align}
\vY = \vX\beta + \vU
\end{align}

それぞれの行列は以下で構成されています。

\begin{align}
\vY = \underbrace{\begin{pmatrix}
Y_1 \\
\vdots \\
Y_N
\end{pmatrix}}_{N \times 1},\;\;
\vX = \begin{pmatrix}
X_{1}'\\
\vdots \\
X_{N}'
\end{pmatrix}
= \underbrace{\begin{pmatrix}
X_{1, 1} & \cdots & X_{1, J}\\
\vdots & \ddots & \vdots \\
X_{N, 1} & \cdots & X_{N, J}
\end{pmatrix}}_{N \times J},\;\;
\vU = \underbrace{\begin{pmatrix}
U_1 \\
\vdots \\
U_N
\end{pmatrix}}_{N \times 1}
\end{align}

標準的な仮定として $\E{\vU \mid \vX} = 0$ をおきます。
また、話を簡単にするために、分散均一性 $\var{\vU \mid \vX} = \sigma^2\vI_N$ も仮定しておきます。

OLS推定量

このとき、最小二乗法（Ordinary Least Squares）を用いた推定量は以下で与えられます。

\begin{align}
\hbeta &= \arg\min_{\beta} \paren{\vY - \vX\beta}'\paren{\vY - \vX\beta}\\
&=\inv{\vX'\vX}\vX'\vY
\end{align}

これをOLS推定量と呼びます。
いま興味があるのは、このOLS推定量の信頼度と多重共線性の関係です。
この記事では、多重共線性があるとOLSを推定量の信頼性が低くなっていくことを示します。

まず第一に、もし完全な多重共線性が発生していると、 $\vX'\vX$ がランク落ちして逆行列が取れません。
よって、完全な多重共線性がある場合はそもそも回帰係数が推定できないということになります。
これは多重共線性が最も問題になるケースです。
この場合、完全な多重共線性を回避すべく余計な説明変数を削除するなどの調整が必要になります。

以下では、完全な多重共線性は起きていないとして話を進めます。
つまり、 $\vX'\vX$ がフルランクであることを仮定します。
$\vY = \vX\beta + \vU$ だったことを思い出すと、OLS推定量 $\hbeta$ は以下のように変形できます。

\begin{align}
\hbeta &= \inv{\vX'\vX}\vX'\paren{\vX\beta + \vU}\\
&= \inv{\vX'\vX}\vX'\vX\beta + \inv{\vX'\vX}\vX'\vU\\
&= \beta + \inv{\vX'\vX}\vX'\vU
\end{align}

この変形からOLSを推定量に関する重要な指標である期待値と分散を知ることができます。
まずは期待値をとると、 $\E{\vU \mid \vX} = 0$ の仮定のおかげで

\begin{align}
\E{\hbeta \mid \vX} &= \beta + \inv{\vX'\vX}\vX'\E{\vU \mid \vX}\\
&= \beta
\end{align}

となり、OLS推定量の期待値は真の回帰係数 $\beta$ と一致することがわかります。
この性質は不偏性と呼ばれています。

また、OLS推定量の分散は

$\begin{align} \var{\hbeta_j \mid \vX} &= \var{\inv{\vX'\vX}\vX'\vU \mid \vX}\\ &= \inv{\vX'\vX}\vX'\var{\vU \mid \vX}\vX\inv{\vX'\vX}\\ &= \inv{\vX'\vX}\vX'\sigma^2\vI_N\vX\inv{\vX'\vX}\\ &= \inv{\vX'\vX}\sigma^2 \end{align}$

となることがわかります。
ここで、分散均一性の仮定 $\var{\vU \mid \vX} = \sigma^2\vI_N$ を使っていることに注意して下さい。

推定量の分散はその推定量がどのくらい安定しているのかを表す指標と言えます。
実際、推定量の分散の平方根をとったものは標準誤差と呼ばれていて、信頼区間の計算や統計的仮説検定に利用します。

ところで、いま知りたいことは、多重共線性と推定量の信頼度（＝分散）の関係でした。
残念ながら、 $\var{\hbeta_j \mid \vX} = \inv{\vX'\vX}\sigma^2$ という式からは多重共線性がある場合に分散がどうなるのかいまいち想像ができません。
そこで、 $\var{\hbeta_j \mid \vX}$ を別の形で表現することにします。

Annihilator Matrix

後の行列操作を楽にするために、Annihilator Matrix $\mM$ を導入します（これがなぜAnnihilatorと呼ばれているのかはよくわかりません）。

\begin{align}
\mM = \vI_N - \vX\inv{\vX'\vX}\vX'
\end{align}

行列 $\mM$ は以下の性質を持ちます。
かなり便利なのでこの記事を読む間だけ覚えておいてください。

$\mM' = \mM$ ：転地しても同じ行列
$\mM\mM = \mM$ ：かけても同じ行列
$\mM\vX = 0$ ：説明変数にかけるとゼロ
$\mM\vY = \vY - \vX\hbeta = \hvU$ ：目的変数にかけると残差になる

実際、簡単な行列計算から上記の性質が成り立っていることが見て取れます。

\begin{align}
\mM'
&= \paren{ \vI_N - \vX\inv{\vX'\vX}\vX'}' \\
&= \vI_N - \vX\inv{\vX'\vX}\vX' \\
&= \mM\\
\mM\mM
&= \paren{ \vI_N - \vX\inv{\vX'\vX}\vX'}\paren{\vI_N - \vX\inv{\vX'\vX}\vX'} \\
&= \vI_N - \vX\inv{\vX'\vX}\vX' - \vX\inv{\vX'\vX}\vX' + \vX\inv{\vX'\vX}\vX' \\
&= \mM\\
\mM\vX &= X - \vX\inv{\vX'\vX}\vX'\vX \\
&= 0\\
\mM\vY &= Y - \vX\inv{\vX'\vX}\vX'\vY \\
&= \vY - X\hbeta\\
&= \hvU
\end{align}

$\mM\vY = \vY - \vX\hbeta = \hvU$ という性質から、 $\mM$ は線形回帰モデルの残差を作る行列として知られています。

OLS推定量の別表現

それでは、残差を作る行列 $\mM$ を用いてOLS推定量を別の形で表現できることを示します。
まず、線形回帰モデルを説明変数 $\vXj$ に関する部分と、それ以外の部分 $\vXmj$ に分解します。

\begin{align}
\vY = \vXj\beta_j + \vXmj\betamj + \vU
\end{align}

ここで、それぞれの行列は以下を表しています。

\begin{align}
\vXj &= (X_{1, j}, \dots, X_{N, j})'\\
\vXmj &= (\vX_1, \dots, \vX_{j-1}, \vX_{j+1}, \dots \vX_{J})\\
\betamj &= (\beta_1, \dots, \beta_{j-1}, \beta_{j+1}, \dots \beta_{J})'
\end{align}

いま、説明変数 $\vXj$ に対するOLS推定量 $\hbeta_j$ を知りたいとします。
通常の最小二乗法はすべての $\beta$ を同時に動かして二乗誤差を最小にしますが、
まず $\betamj$ を動かして二乗誤差を最小にし、残った部分に対して改めて $\beta_j$ を動かして二乗誤差を最小にする $\hbeta_j$ を求める、という二段階のステップを踏んでも同じ結果になります。
この操作を数式で表現すると以下になります。

\begin{align}
\hbeta_j &= \arg\min_{\beta_j}\brac{\min_{\betamj}\paren{\vY - \vXj\beta_j - \vXmj\betamj}'\paren{\vY - \vXj\beta_j - \vXmj\betamj}}
\end{align}

内側の最小化問題をよく見ると、これは $\vY - \vXj\beta_j$ に対して $\vXmj\betamj$ で回帰していると解釈できるので、そのOLS推定量は以下で求めることができます。

\begin{align}
\hbetamj &= \inv{\vXmj'\vXmj}\vXmj'\paren{\vY - \vXj\beta_j}
\end{align}

これを内側の最小化問題に戻すことを考えると

\begin{align}
\vY - \vXj\beta_j - \vXmj\hbetamj
&= \vY - \vXj\beta_j - \vXmj\inv{\vXmj'\vXmj}\vXmj'\paren{\vY - \vXj\beta_j}\\
&= \paren{\vI_N - \vXmj\inv{\vXmj'\vXmj}\vXmj'}\paren{\vY - \vXj\beta_j}\\
& = \mMmj\paren{\vY - \vXj\beta_j}\\
&= \mMmj\vY - \mMmj\vXj\beta_j
\end{align}

なので、元の最小化問題は

\begin{align}
\hbeta_j &= \arg\min_{\beta_j}\paren{\mMmj\vY - \mMmj\vXj\beta_j}\paren{\mMmj\vY - \mMmj\vXj\beta_j}
\end{align}

となることが分かります。

ここから、OLS推定量は

\begin{align}
\hbeta_j &= \inv{\vXj'\mMmj'\mMmj\vXj}\vXj'\mMmj'\mMmj\vY\\
&= \inv{\vXj'\mMmj\vXj}\vXj'\mMmj\vY\\
\end{align}

という形式でも表現できることがわかりました。

補助回帰

OLS推定量を別形式で表現できましたが、ここに出てくる $\mMmj\vXj$ は何を計算しているのでしょうか？
残差を作る行列 $\mMmj$ の意味を考えると、 $\mMmj\vXj$ は説明変数 $\vXj$ を他の説明変数 $\vXmj$ で回帰したときの残差を表しています。
つまり、線形回帰モデル

\begin{align}
\vXj = \vXmj\gamma + \vVj
\end{align}

に対する残差

\begin{align}
\mMmj\vXj = \vXj - \vXmj\inv{\vXmj'\vXmj}\vXmj'\vXj = \vXj - \vXmj\hgamma = \hvVj
\end{align}

を表現しています。
説明変数 $\vXj$ をその他の説明変数 $\vXmj$ で回帰することは補助回帰（auxiliary regression）と呼ばれています。
残差が $\hvVj$ 小さければ、説明変数 $\vXj$ は他の説明変数 $\vXmj$ でほぼ表現できてしまうということになります。
この場合、説明変数 $\vXj$ は追加的に与える情報量の少ない説明変数ということになります。
一方で、残差が $\hvVj$ が大きい場合は、説明変数 $\vXj$ は他の説明変数では与えることのできない情報をモデルに与えていると言えます。

これを多重共線性の文脈でいうと、残差 $\hvVj$ が小さいことは（説明変数 $\vXj$ に対する）多重共線性が強いことに対応し、残差 $\hvVj$ が大きいことは多重共線性が弱いことに対応します。
実際、完全な多重共線性がある状態として $\vXj = \vX_k$ となるような別の特徴量が存在するケースを考えると、残差 $\hvVj$ もゼロになります。

OLS推定量の分散を解釈する

それでは、改めてOLS推定量の分散について考えましょう。
$\vY = vXj\beta_j + \vXmj\betamj + \vU$ であったことを思い出すと、OLS推定量は以下のように変形できます。

\begin{align}
\hbeta_j &= \inv{\vXj'\mMmj \vXj}\vXj'\mMmj\paren{\vXj\beta_j + \vXmj\betamj + \vU}\\
&= \underbrace{\inv{\vXj'\mMmj \vXj}\vXj'\mMmj\vXj}_{=\vI_J}\beta_j
+ \inv{\vXj'\mMmj \vXj}\vXj'\underbrace{\mMmj\vXmj}_{=0}\betamj
+ \inv{\vXj'\mMmj \vXj}\vXj'\mMmj\vU\\
&= \beta_j + \inv{\vXj'\mMmj \vXj}\vXj'\mMmj\vU\\
&= \beta_j + \inv{\vXj'\mMmj\mMmj\vXj}\vXj'\mMmj\mMmj\vU\\
&= \beta_j + \inv{\hvVj'\hvVj}\hvVj'\vU
\end{align}

これの分散をとると

$\begin{align} \var{\hbeta_j \mid \vX} &= \var{\inv{\hvVj'\hvVj}\hvVj'\vU \mid \vX}\\ &= \inv{\hvVj'\hvVj}\hvVj'\var{\vU \mid \vX}\hvVj\inv{\hvVj'\hvVj}\\ &= \inv{\hvVj'\hvVj}\hvVj'\sigma^2\vI_N\hvVj\inv{\hvVj'\hvVj}\\ &= \inv{\hvVj'\hvVj}\sigma^2 \end{align}$

となります。
さらに、 $\hvVj'\hvVj = \sumi \hVij^2 = \sumi\quad{\Xij - \hXij}$ であることを利用すると、

$\begin{align} \var{\hbeta_j \mid \vX} &= \frac{\sigma^2}{\sumi\quad{\Xij - \hXij}} \end{align}$

と表現できます。
説明変数 $\vXj$ の平均を $\bXj = \frac{1}{N}\sumi X_{i, j}$ として、分母に $\sumi \quad{\Xij - \bXj}$ をかけて割ると

$\begin{align} \var{\hbeta_j \mid \vX} &= \frac{\sigma^2}{\sumi \quad{\Xij - \hXij} / \sumi \quad{\Xij - \bXj}} \times \frac{1}{N \times \frac{1}{N}\sumi \quad{\Xij - \bXj}}\\ &= \frac{\sigma^2}{N\paren{1 - R^2_j}\hvar{X_j}} \end{align}$

を得ます。
ここで、
\begin{align}
R^2_j = 1 - \frac{\sumi \quad{\Xij - \hXij}}{\sumi \quad{\Xij - \bXj}}
\end{align}
は説明変数 $\vXj$ をその他の説明変数 $\vXmj$ で回帰したときの決定係数です。 $\vXj$ のばらつきのうち平均では説明できなかった部分を $\vXmj$ でどのくらい説明できるかを表しています。つまり、多重共線性の強さを表す指標です。ちなみに、 $\vXmj$ が一変数の場合は相関係数の二乗に相当します。

また、 $\hvar{X_j}$ は説明変数 $\vX_j$ の標本分散を表しています。

さて、ここまで長い道のりでしたが、この表現から多重共線性がOLS推定量の分散（信頼度）にどう影響するかを解釈することができます。

1. 説明変数 $\vX$ では説明できない目的変数 $\vY$ の変動 $\sigma^2$ が大きければ大きいほど、分散が大きくなる
2. サンプルサイズ $N$ が大きくなると、分散が小さくなる
3. 説明変数 $\vX_j$ の標本分散 $\hvar{X_j}$ が大きくなると、分散が小さくなる
4. 決定係数 $R^2_j$ が大きくなると、分散が大きくなる

1.はデータの限界みたいなところがあるので言っても仕方ないかなと思っています。

2.は当たり前といえば当たり前で、データが多いと推定量の信頼性が上がっていくのはよく言われていることですね。
ただ、 $\var{\hbeta_j \mid \vX} = \inv{\vX'\vX}\sigma^2$ という表現からは明示的には見えてこなかった部分ではあります。

3.は説明変数の取りうる値のレンジが大きいと回帰係数が小さくなることからくる性質なので、これもあんまり気にしなくていいと思います。
実際、説明変数をあらかじめ標準化すると分散が1になるので無視できます。
これも $\var{\hbeta_j \mid \vX} = \inv{\vX'\vX}\sigma^2$ という表現からは明示的には見えてこなかった部分ではあります。

やはり重要なのは4.で、説明変数 $\vXj$ をその他の説明変数 $\vXmj$ で説明できてしまう割合が大きいと、OLS推定量 $\hbeta_j$ の信頼性が下がることが見て取れます。
つまり、多重共線性があるケースで推定量の信頼性が下がることがわかります。
ここで重要なことは、 $\hbeta_j$ の信頼性に影響するのはあくまで $\hbeta_j$ に対する決定係数 $R_j^2$ であることです。
言い換えると、 $\vXj$ とは関係ない説明変数同士で強い相関があったとしても、それらの説明変数が $\vXj$ に対して説明力を持たないのであれば、 $\hbeta_j$ の信頼性に特に影響は与えません。
ですので、多重共線性を考える際には、あくまでいま興味のあるターゲットの説明変数 $\vXj$ に対する多重共線性のみに注意すればよく、他の説明変数で多重共線性が起きていても（その説明変数の回帰係数に興味がないなら）無視しても良いと言えます。

これが特に重要になってくるのは因果関係を考えるケースで、多重共線性を気にしてコントロール変数をむやみにモデルから外すと欠落変数バイアスが発生してしまいます。
ターゲットの説明変数と無関係の多重共線性は気にせず、論理的に入れるべきコントロール変数は入れるべきだと思います。
ターゲットの説明変数に対して強い多重共線性が発生しているケースは問題といえば問題だとは思うのですが、そもそもコントロール変数でほとんどの部分が説明できてしまう変数をターゲットにするのはどうなんだという話にもなるかなと思っています。

まとめると、完全な多重共線性はそもそも計算ができないので問題ですが、そうでなければ多重共線性はあまり気にしなくていいケースがほとんどだと思っています。

シミュレーションによる信頼度の確認

シミュレーションの設定

OLS推定量の分散の振る舞いを数式からも確認しましたが、ここではシミュレーションを用いて理解を深めることにします。
以下の設定でシミュレーションデータを生成します。

$\begin{align} Y &= X_0 + X_1 + X_2 + U\\ (X_0, X_1, X_2) &\sim \mathcal{N}\paren{ \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix},\; \begin{pmatrix} 1 & \rho & 0\\ \rho & 1 & 0\\ 0 & 0 & 1 \end{pmatrix} }\\ U &\sim \mathcal{N}\paren{0, \sigma^2} \end{align}$

ここで、説明変数 $X_0$ と $X_1$ は相関していて、 $X_2$ は無相関であるような設定を考えています。
話を単純にするために、回帰係数 $(\beta_0, \beta_1, \beta_1)$ はすべて1としています。

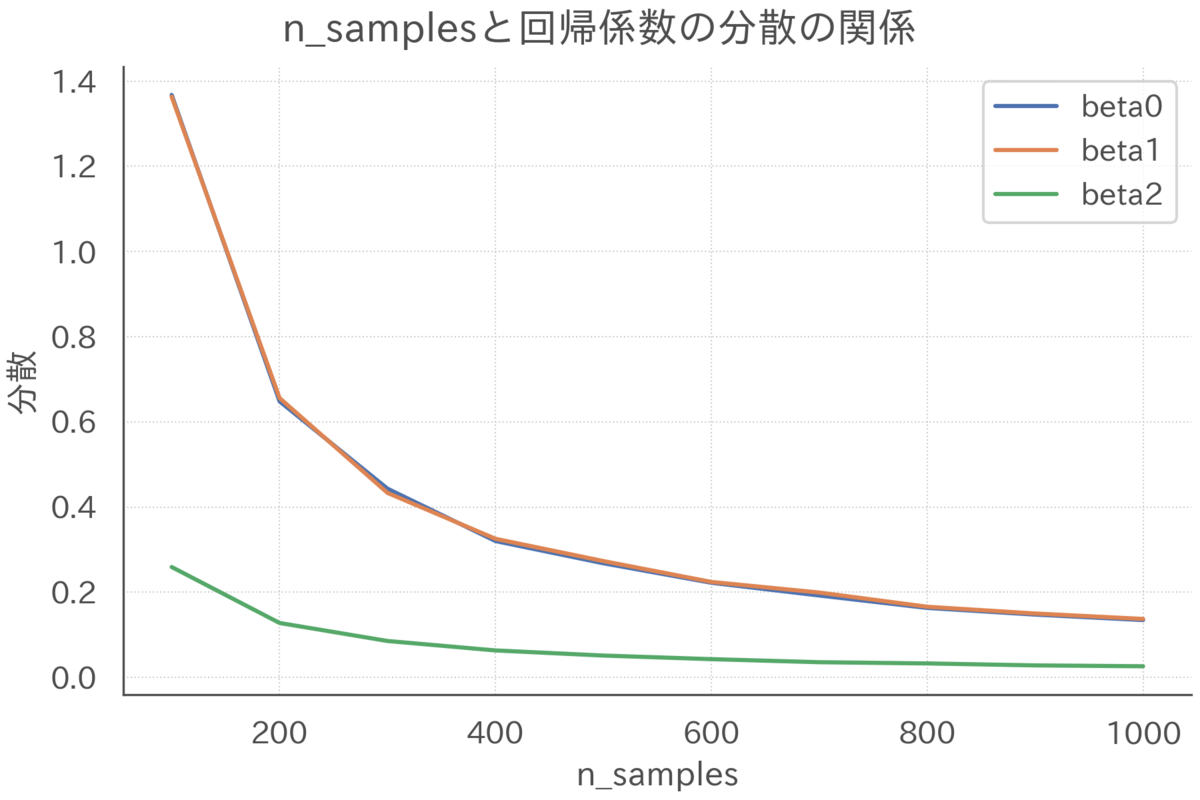
多重共線性とOLS推定量の信頼度

まずは多重共線性がOLS推定量の分散に与える影響を見ていきます。
多重共線性の強さによる影響の大きさを知るために、説明変数 $X_0$ と $X_1$ の相関係数 $\rho$ を変化させた場合の分散の大きさを確認します。

f:id:dropout009:20210722194753p:plain

上図を確認すると、説明変数 $(X_0, X_1)$ の相関が強くなるにつれて、 $(\beta_0, \beta_1)$ に関するOLS推定量の分散 $\hvar{\beta_0 \mid \vX}$ と $\hvar{\beta_1 \mid \vX}$ が大きくなっていく様子が見て取れます。
よって、多重共線性が強くなると推定量の信頼性は低くなると言えます。

一方で、説明変数 $(X_0, X_1)$ の相関は、 $\beta_2$ に関するOLS推定量の分散 $\hvar{\beta_2 \mid \vX}$ にはなんの影響も与えていないこともわかります。
数式でも確認したように、もし回帰係数 $\beta_2$ にのみ興味がある場合は、説明変数 $(X_0, X_1)$ の多重共線性は無視してモデルに含めてもいいことがわかりました。

サンプルサイズとOLS推定量の信頼度

f:id:dropout009:20210722194757p:plain

次に、相関係数 $\rho$ を0.9で固定したままサンプルサイズが変化した場合のOLS推定量の分散を可視化したものが上図になります。
強い多重共線性があるぶん $(\beta_0, \beta_1)$ の信頼度は高めになっていますが、それでもサンプルサイズを大きくれば分散が小さくなっていく様子が見て取れます。
逆に言うと、興味のある説明変数に多重共線性が存在している場合は、できるだけたくさんデータを集める必要があることがわかります。

リッジ推定量で推定量の信頼性を高める

リッジ推定量の導入

ここまで、強い多重共線性が存在すると回帰係数の推定が安定せずOLS推定量 $\hbeta$ の信頼度が下がる（分散が大きくなる）ことを、数式とシミュレーションの両面から見てきました。
推定量の信頼度が低いと、回帰分析を用いた意思決定の信頼度が下がることに繋がります。

そこで、推定量の分散を抑える手法として、リッジ回帰（Redge Regression）という手法が知られています。
この手法では、最小二乗法を行う際の損失関数に、 $\beta$ が大きいほど強い罰則を与える罰則項を加えます。
この罰則によって、推定量は極端に大きな値を取らないような制限がかかり、推定が安定します。

\begin{align}
\hbeta(\lambda) &= \arg\min_{\beta} \paren{\vY - \vX\beta}'\paren{\vY - \vX\beta} + \lambda \beta'\beta\\
&= \inv{\vX'\vX + \lambda \vI_J}\vX'\vY
\end{align}

このような罰則を加えた推定量はリッジ推定量と呼ばれています*3。
ここで、 $\lambda$ は罰則の強さを表しています。
$\beta'\beta = \|\beta\|^2_2$ はL2ノルムによる罰則と解釈できることから、これはL2正則化とも呼ばれています。

OLS推定量と比較して、 $\lambda \vI_J$ の項目が分母にある分、リッジ推定量のほうが（絶対値でみて）小さい値になります。
$\lambda$ が大きいほど強い罰則がかかり、 $\beta$ が0方向に引っ張られます。
実際 $\lambda$ を無限大に飛ばすと推定量は0になります。
逆に、 $\lambda = 0$ のときは、リッジ推定量はOLS推定量と一致します。

リッジ推定量の性質

それでは、リッジ推定量の性質を確認するため、その期待値と分散を計算します。

変換行列の準備

後の話を簡単にするため、OLS推定量をリッジ推定量に変換する行列 $\mW$ を定義しておきます。

\begin{align}
\mW\hbeta &=\hbeta(\lambda)
\end{align}

行列 $\mW$ の中身を知りたいので、OLS推定量とリッジ推定量を代入します。

\begin{align}
\mW\hbeta &=\hbeta(\lambda) \\
\mW \inv{\vX'\vX}\vX'\vY&= \inv{\vX'\vX + \lambda \vI_J}\vX'\vY
\end{align}

両辺に $\inv{\vX'\vY}\paren{\vX'\vX}$ を右からかけてあげると $\mW$ の中身がわかります。

\begin{align}
\mW \inv{\vX'\vX}\vX'\vY\inv{\vX'\vY}\paren{\vX'\vX} &= \inv{\vX'\vX + \lambda \vI_J}\vX'\vY\inv{\vX'\vY}\paren{\vX'\vX}\\
\mW&= \inv{\vX'\vX + \lambda \vI_J}\paren{\vX'\vX}
\end{align}

リッジ推定量の期待値

さて、この変換行列 $\mW$ を用いてリッジ推定量の期待値を計算します。

\begin{align}
\E{\hbeta(\lambda) \mid \vX}
&= \E{\mW\hbeta \mid \vX}\\
&= \mW\E{\hbeta \mid \vX}\\
&= \inv{\vX'\vX + \lambda \vI_J}\paren{\vX'\vX}\beta\\
&\leqslant \beta
\end{align}

OLS推定量とは異なり、リッジ推定量の期待値は真の回帰係数 $\beta$ と一致しません。
分母の $\lambda \vI_J$ の分だけ0方向にバイアスがかかることがわかります。
よって、罰則の強さ $\lambda$ を大きくすればするほどバイアスは大きくなります。

推定量にバイアスがかかるのはあまりうれしくない性質です。
ただ、バイアスの方向がゼロに向かうのは、実務的にはそんなに悪くない性質だと思っています。
というのも、ゼロ方向にバイアスがかかるというのは、説明変数が目的変数に与える効果を「過小評価」するという話なので、リッジ回帰で過小評価されていてもなお十分に効果があるなら、保守的に見てもそのくらいの効果がある可能性が高い、という判断が可能になるからです。

リッジ推定量の分散

次に、リッジ推定量の分散について確認します。

$\begin{align} \var{\hbeta(\lambda) \mid \vX} &= \var{\mW\hbeta \mid \vX}\\ &= \mW\var{\hbeta \mid \vX}\mW'\\ &= \inv{\vX'\vX + \lambda \vI_J}\paren{\vX'\vX}\inv{\vX'\vX}\sigma^2\paren{\vX'\vX}\inv{\vX'\vX + \lambda \vI_J}\\ &= \inv{\vX'\vX + \lambda \vI_J}\paren{\vX'\vX}\inv{\vX'\vX + \lambda \vI_J}\sigma^2 \end{align}$

$\mW$ は分母のほうが大きいので、リッジ推定量の分散はOLS推定量の分散より小さくなることがわかります。また、 $\lambda$ を大きくすれば分散が小さくなることも見て取れます。

まとめると、リッジ推定量は、バイアスがかかることを代償に推定量の信頼性を高める手法であると解釈できます。
このバイアスと信頼性の関係はBias-Variance tradeoffとして機械学習や統計学の分野で知られています。

シミュレーションによる確認

リッジ推定量についても、罰則の強さによって期待値と分散がどのように変化するかシミュレーションで確認しておきます。

まずは期待値について確認します。サンプルサイズを200、相関係数を0.99で固定して、罰則の強さ $\lambda$ だけを変化させた場合のリッジ推定量の期待値を可視化します。
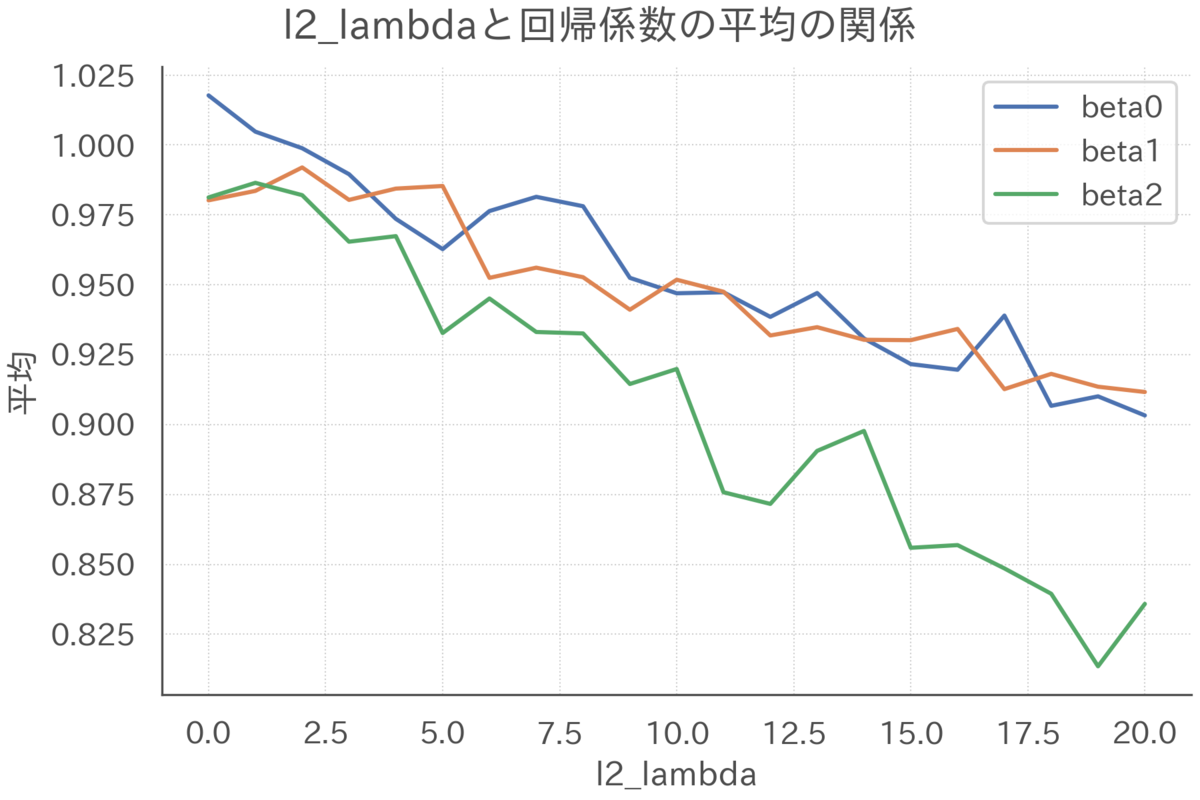
f:id:dropout009:20210722194802p:plain

回帰係数はすべて1だったことを念頭に置いて上図を確認すると、 $\lambda$ を大きくするにつれてリッジ推定量は0方向にひっぱられてバイアスが強くなっていくことがわかります（サンプルサイズが小さく多重共線性が強いので、罰則ゼロのときそもそもあんまりうまく推定できていないことも見て取れます）。

同様の設定でリッジ推定量の分散を確認します。
f:id:dropout009:20210722194808p:plain

罰則を強くすると推定量の分散が小さくなっていく様子が見て取れます。
このように、リッジ推定量はバイアスという犠牲を払って信頼性を高めることができます。

まとめ

この記事では、多重共線性がOLS推定量の信頼性に与える影響について、数式とシミュレーションの両面から確認しました。
大雑把に言うと、完全な多重共線性があるケースを除いて、興味のある説明変数以外の多重共線性はあまり気にしなくて良いことがわかりました。

また、推定量の信頼性を高める手法の一つとして、リッジ推定量を紹介しました。
リッジ推定量はゼロ方向にバイアスがかかりますが、推定量の分散を小さくできることを確認しました。
リッジ推定量には、例えば説明変数の数 $J$ がサンプルサイズ $N$ よりも大きくても推定が可能になるなど、他にも便利な性質がいくつかあります。リッジ推定量の詳細はvan Wieringen(2015)をご確認ください。

この記事で利用したシミュレーションコードは以下になります。
github.com

参考文献

Hansen, Bruce E. "Econometrics." (2021). https://www.ssc.wisc.edu/~bhansen/econometrics/.
van Wieringen, Wessel N. "Lecture notes on ridge regression." arXiv preprint arXiv:1509.09169 (2015).

*1:僕が受講した計量経済学のコースワークは市村英彦先生が担当されていたのですが、講義ノートにはしっかり記述がありました。

*2:Hansen(2011)を特に参考にしています。

*3:リッジ推定量の利点として、完全な多重共線性が存在するケースでも逆行列がとれるので推定が可能になることが挙げられたりしています。それは実際そうなんですが、完全な多重共線性があってしかも回帰係数に興味がある場合はリッジ回帰で対処するのではなく手作業で完全な多重共線性を排除したほうがいいと思います。

2021-07-19

Influence Functionでインスタンスの重要度を解釈する

interpretable machine learning Python influence 機械学習シミュレーション

$\def\paren#1{\left(#1\right)} \def\sumi{\sum_{i=1}^N} \def\htheta{\hat{\theta}} \def\hthetami{\htheta_{- i}} \def\hthetamie{\hthetami(\epsilon)} \def\nablat{\nabla_{\theta}} \def\nablatt{\nabla_{\theta}^2} \def\evale#1{\left.#1\right|_{\epsilon=0}}$

モチベーション
- インスタンス重要度の定義は？
- Leave One Outによるインスタンス重要度の計算
Influence Functionでインスタンス重要度を近似する
- 記法の導入
- Influence Functionの導出
  - パラメータの性質
線形回帰モデルの場合
- 線形回帰モデルのInfluence Function
- シミュレーション
まとめ
参考文献

モチベーション

Permutation Feature Importance（PFI）、Partial Dependence（PD）、Accumulated Local Effects（ALE）などの機械学習の解釈手法は、特徴量とモデルの予測値の関係を通じて機械学習モデルを解釈する手法でした*1。
たとえば、PFIでは「どの特徴量がモデルにとって重要なのか」という視点でブラックボックスモデルに解釈性を与えることが出来ます。
特徴量重要度の用途の一つはデバッグです。
ドメイン知識から考えると不自然な重要度をもつ特徴量が存在すれば、データやモデルに不備があるのかもしれません。
また、重要度が極端に高い特徴量は、何か情報がリークしている可能性があります。

このように、「どの特徴量がモデルにとって重要なのか」を知ることはモデルの振る舞いを解釈する上で重要です。
ここでは特徴量に注目していますが、視点を変えてインスタンスに注目することもできます。
つまり、「どのインスタンスがモデルにとって重要なのか」という解釈性も、機械学習モデルの振る舞いを理解する上で役に立ちそうです。
このような解釈性を、特徴量重要度に対比してインスタンス重要度とこの記事では呼ぶことにします。
特徴量重要度と同様にモデルのデバッグを考えると、極端に重要度の高いインスタンスが存在すれば、そのインスタンスを外れ値として除外する、そもそもデータとしておかしいのではないか確認するなどの対応が取れます。

インスタンス重要度の定義は？

「どのインスタンスがモデルにとって重要なのか」を知ることには意味がありそうですが、これを知るためにはそもそも何をもって重要とみなすかをきちんと定義する必要があります。
できればどんなモデルに対しても重要度を計算したいので、すべてのモデルが共通に持っている要素である「予測値」に注目します。つまり、「そのインスタンスの有無でモデルの予測がどのくらい大きく変わるか」をもって重要度を定義します。

具体例として、下図を見てください。
右下の外れ値を学習データに入れた場合と入れなかった場合での線形回帰の予測線を可視化しています。
外れ値を入れると回帰直線の傾きが緩やかになることが見て取れます。

f:id:dropout009:20210718020515p:plain

上記画像とシミュレーションデータを作成するためのコードは以下になります。

def generate_simulation_data(
    n_incetances: int,
) -> tuple[np.ndarray, np.ndarray]:
    """シミュレーションデータを生成する"""

    x = np.random.normal(0, 1, n_incetances)
    u = np.random.normal(0, 0.1, n_incetances)

    y = x + u

    # 外れ値で上書きする
    x[0] = 2
    y[0] = -2

    return (x, y)


x, y = generate_simulation_data(n_incetances=20)

def draw_regression_line(x: np.ndarray, y: np.ndarray) -> None:
    """外れ値を含んだ場合と含まない場合の回帰直線を可視化する"""

    fig, ax = plt.subplots()
    sns.regplot(x, y, scatter_kws=dict(alpha=1), ci=None, ax=ax)
    sns.regplot(x[1:], y[1:], scatter_kws=dict(alpha=1), color=".7", ci=None, ax=ax)
    ax.set(xlabel="X", ylabel="Y")
    fig.suptitle("外れ値による回帰直線の変化")
    fig.savefig(f"output/outlier.png")
    fig.show()


draw_regression_line(x, y)

Leave One Outによるインスタンス重要度の計算

このように、そのインスタンスを学習データに含めることでどれだけ予測値が変化するのか、そしてその結果としてどれだけ予測精度が変化するのかを計算し、それをインスタンスの重要度とすることができそうです。
この重要度計算アルゴリズムは、インスタンスをひとつずつ取り除いて（Leave One Out, LOO）繰り返し学習と予測を行うだけなので、簡単に実装することが出来ます。

def calc_leave_one_out_error_diff(x: np.ndarray, y: np.ndarray) -> np.ndarray:
    """LOOでの予測誤差の差分を計算する"""

    n_incetances = x.shape[0]
    X = x.reshape(-1, 1)
    y_pred = LinearRegression().fit(X, y).predict(X)

    error_diff = np.zeros((n_incetances, n_incetances))
    for i in range(n_incetances):
        X_loo = np.delete(X, i, 0)
        y_loo = np.delete(y, i, 0)

        y_pred_loo = LinearRegression().fit(X_loo, y_loo).predict(X)
        error_diff[:, i] = (y - y_pred_loo) ** 2 - (y - y_pred) ** 2

    return error_diff


looed = calc_leave_one_out_error_diff(x, y)
avg_diff = looed.mean(0) # 平均的な誤差を計算

計算結果を可視化してみると、先程の画像で右下に位置していたインスタンス0がモデルの予測に最も大きな影響を与えていたことがわかります。

def draw_importance(imp: np.ndarray) -> None:
    """インスタンスごとの重要度を可視化する"""

    df = (
        pd.DataFrame({"importance": imp})
        .reset_index()
        .rename({"index": "instance"}, axis=1)
        .sort_values("importance")
        .reset_index(drop=True)
        .assign(instance=lambda df: df.instance.astype(str))
    )
    
    fig, ax = plt.subplots()
    ax.barh(df["instance"], df["importance"])
    ax.set(xlabel="重要度", ylabel="インスタンスNo.")
    fig.suptitle("インスタンスごとの重要度")
    fig.savefig(f"output/imp.png")
    fig.show()


draw_importance(avg_diff)

f:id:dropout009:20210718020459p:plain

Influence Functionでインスタンス重要度を近似する

記法の導入

LOOによる予測誤差の変化は直感的でわかりやすいですが、インスタンス重要度の計算に再学習が必要なので計算に時間がかかることが欠点です。
今回のシミュレーションではインスタンスの数が20でモデルは線形回帰だったのですぐに計算は終わりましたが、実務の際にはより大量のデータをより複雑なモデルで分析します。
ですので、より複雑な問題に取り組む際には、再学習を必要としないアルゴリズムが必要になります。

実は、Influence Functionを利用して、再学習を行わずにインスタンス重要度を近似計算するアルゴリズムがKoh and Liang(2017)で提案されています。
ここで、このアルゴリズムを記述するためにいくつかの記法を導入します。

特徴量とアウトカムの組を $z = (x, y)$ とします
モデルはパラメトリックなモデルを採用し、そのパラメータを $\theta$ で表します。パラメータは $K$ 個あるとします。つまり、 $\theta = (\theta_1, \dots, \theta_K)$ とします
損失関数を $L(z, \theta) = L(y, f(x, \theta))$ で定義します。モデルが線形回帰で損失関数が二乗誤差なら $L(z, \theta)=\paren{y - x^\top\theta}^2$ です
データに対する予測誤差の総和を $R(\theta) = \sumi L(z_i, \theta)$ で表します。モデルが線形回帰で損失関数が二乗誤差なら $R(\theta)=\sumi\paren{y_i - x_i^\top\theta}^2$ です

さて、モデルは予測誤差が最も小さくなるようにパラメータ $\theta$ を選びます。
つまり、全インスタンスを学習した場合のパラメータ $\htheta$ は
\begin{align}
\htheta = \arg\min_{\theta \in \Theta}\sumi L(z_i, \theta)
\end{align}
であり、インスタンス $i$ を取り除いたデータで学習した場合のパラメータ $\hthetami$ は
\begin{align}
\hthetami = \arg\min_{\theta \in \Theta} \sum_{j \neq i} L(z_j, \theta)
\end{align}
となります。

この記法を用いると、インスタンス $i$ を使わずにモデルの学習を行った場合に、インスタンス $j$ の予測誤差に与える影響は以下のように表現できます。
\begin{align}
L\paren{z_j, \hthetami} - L\paren{z_i, \htheta}
\end{align}
ここで、

$L\paren{z_j, \hthetami}$ はインスタンス $i$ を取り除いたデータで学習を行い、インスタンス $j$ を予測した場合の誤差
$L\paren{z_i, \htheta}$ は全データで学習を行い、インスタンス $j$ を予測した場合の誤差

を表します。この差分が大きいほどインスタンスの重要度は高くなります。

Influence Functionの導出

前述のように、このようなLOOによるインスタンス重要度の計算はモデルの再学習が必要なので時間がかかるという問題がありました。
これを克服するためには、モデルの再学習を行わなずに再学習を行った場合の結果を近似できるような手法を考える必要があります。

そこで、Koh and Liang(2017)では以下のような最小化問題を導入しました。
\begin{align}
\hthetamie = \arg\min_{\theta \in \Theta} \sumi L(z_j, \theta) - \epsilon L(z_i, \theta)
\end{align}

ここで、 $\epsilon L(z_i, \theta)$ という項が追加されていることに注意してください。
この項に注目すると、以下の性質があることが見て取れます。

$\epsilon = 0$ のとき、全インスタンスを用いた最小化問題と一致する。つまり、 $\hthetami(0) = \htheta$
$\epsilon = 1$ のとき、インスタンス $i$ を取り除いた最小化問題と一致する。つまり、 $\hthetami(1) = \hthetami$

$\epsilon \in (0, 1)$ の場合は、インスタンス $i$ を完全に取り除いた（重みをゼロにした）状態や、全データを用いた状態ではなく、インスタンス $i$ の重みをちょっとだけ（ $\epsilon$ だけ）軽くした状態を考えています。
よって、 $\epsilon$ はインスタンス $i$ の重みをコントロールするパラメータと解釈できます。重みが1のときはインスタンス $i$ を取り除いてモデルの学習を行うことに、重みが0のときは全インスタンスを用いてモデルの学習を行うことに相当します。

この最小化問題の解として与えられる $\hthetamie$ を用いた場合、任意の $z = (x, y)$ に対する予測誤差は $L(z, \hthetami(\epsilon))$ です。
ここで、 $\epsilon$ を0から少しだけ変化させたときに、どのくらい誤差が変化するかを考えます。
なんでこんなことを考えるのかを平たく言うと以下になります。

ほんとは $\epsilon = 0$ の場合と $\epsilon = 1$ の場合の予測誤差の変化を見たい
→それは再学習が必要になって大変
→それなら $\epsilon$ が0からちょっとだけ変化したときの予測誤差の変化を使って、 $\epsilon$ を1単位変化させた場合の（ $\epsilon = 0$ から $\epsilon = 1$ まで持っていた場合の）予測誤差の変化を近似しよう。 $\epsilon = 1$ のときのパラメータはインスタンス $i$ を取り除いたときの予測誤差なので、この近似によってさも再学習をしたかのようなパラメータを推定できる

上記の操作は予測誤差 $L(z, \hthetami(\epsilon))$ を $\epsilon$ で微分して $\epsilon=0$ で評価すれば実行できます。
\begin{align}
\evale{\frac{d L(z, \hthetami(\epsilon))}{d \epsilon}}
&= \evale{\nablat L(z, \hthetamie)^\top \frac{d \hthetamie}{d\epsilon}}\\
&= \evale{\nablat L(z, \htheta)^\top \frac{d \hthetamie}{d\epsilon}}
\end{align}

ここで、 $\evale{\hthetami(\epsilon)} = \hthetami(0) = \htheta$ であることを利用しています。
上式の $\nablat L(z, \htheta)$ は全データで学習したモデルを用いた予測誤差で求まります。
ですので、残りの $\evale{\frac{d \hthetamie}{d\epsilon}}$ をどうやって求めるかがわかれば、これを計算できます。

パラメータの性質

それでは $\hthetamie$ の性質を調べます。そもそも $\hthetamie$ がどうやって計算されていたかを思い出すと、
\begin{align}
\hthetamie = \arg\min_{\theta \in \Theta} \sumi R(\theta) - \epsilon L(z_i, \theta)
\end{align}
でした。
この後の操作を可能にするために、 $R(\theta)$ は $\theta$ に関してstrongly convexで2階微分可能であることを仮定します*2。

$\hthetamie$ は目的関数を最小化する値なので、1階条件
\begin{align}
\nablat R(\hthetamie) - \nablat L(z_i, \hthetamie)\epsilon = 0
\end{align}
を満たします。

ここで、左辺を $\htheta$ の周りで1階のテイラー展開すると以下を得ます。

\begin{align}
\paren{\nablat R(\htheta) - \nablat L(z_i, \htheta)\epsilon} + \paren{\nablatt R(\htheta) - \nablatt L(z_i, \htheta)\epsilon}\paren{\hthetamie - \htheta} + \mathrm{residual}
\end{align}

ところで、 $\htheta$ は $R(\theta)$ を最小化する値なので、 $\nablat R(\htheta) = 0$ です。ついでに剰余項を無視して近似すると

\begin{align}
0 \approx - \nablat L(z_i, \htheta)\epsilon + \paren{\nablatt R(\htheta) - \nablatt L(z_i, \htheta)\epsilon}\paren{\hthetamie - \htheta}
\end{align}

なので、整理すると

\begin{align}
\paren{\hthetamie - \htheta} \approx \paren{\nablatt R(\htheta) - \nablatt L(z_i, \htheta)\epsilon}^{-1}\nablat L(z_i, \htheta)\epsilon
\end{align}

となります。

$\epsilon$ を $0$ からちょっとだけ動かしたときに $\hthetamie$ が $\htheta$ からどれだけ離れるかを知りたいので、両辺を $\epsilon$ で微分して $\epsilon=0$ で評価します。

\begin{align}
\evale{\frac{d\paren{\hthetamie - \htheta}}{d\epsilon}} \approx& \evale{\paren{\nablatt R(\htheta) - \nablatt L(z_i, \htheta)\epsilon}^{-1}\nablat L(z_i, \htheta)}\\
&+\evale{\paren{\nablatt R(\htheta) - \nablatt L(z_i, \htheta)\epsilon}^{-2}\nablatt L(z_i, \htheta)\nablat L(z_i, \htheta)\epsilon}\\
\evale{\frac{d\hthetamie}{d\epsilon}} &\approx \nablatt R(\htheta)^{-1}\nablat L(z_i, \htheta)
\end{align}

これを元の式に戻すと

\begin{align}
\evale{\frac{d L(z, \hthetami(\epsilon))}{d \epsilon}} \approx \nablat L(z, \htheta)^\top\nablatt R(\htheta)^{-1}\nablat L(z_i, \htheta)
\end{align}

を得ます。上式は $\epsilon$ を1単位動かしたときの予測誤差の変化を1階近似していると解釈できます。 $\epsilon = 0$ と $\epsilon = 1$ の差分は、全データを用いた場合と、インスタンス $i$ を取り除いた場合の予測誤差の差分でした。よって、インスタンス $i$ を取り除いたことによる予測誤差の変化を近似していると解釈できます。

これはInfluence Functionと呼ばれています。インスタンス $i$ を取り除いたときの $z=(x, y)$ に対する予測誤差の変化を

\begin{align}
\mathcal{I}_i(z) = \nablat L(z, \htheta)^\top\nablatt R(\htheta)^{-1}\nablat L(z_i, \htheta)
\end{align}

と表記することにします。

線形回帰モデルの場合

線形回帰モデルのInfluence Function

さて、抽象的な議論が続いてしまったので、具体的に特徴量が1つだけの単純な線形回帰モデル
\begin{align}
y = x\theta + u
\end{align}
を考えます。損失関数は二乗誤差とします。
このとき、Influence Functionに必要なパーツはそれぞれ以下で計算できます。

\begin{align}
L(z, \theta) &= (y - x\theta)^2, \\
\nablat L(z, \theta) &= -2(y - x\theta)x,\\
R(\theta) &= \sumi(y_i - x_i\theta)^2,\\
\nablat R(\theta) &= -2\sumi(y_i - x_i\theta)x_i,\\
\nablatt R(\theta) &= 2\sumi x_i^2,\\
\htheta &= \frac{\sumi x_iy_i}{\sumi x_i^2}
\end{align}

これをInfluence Functionに代入することで、線形回帰モデルに対して再学習無しでインスタンスの重要度を近似することが出来ます*3。

\begin{align}
\mathcal{I}_i(z) &= \nablat L(z, \htheta)^\top\nablatt R(\htheta)^{-1}\nablat L(z_i, \htheta)\\
&= \paren{-2\paren{y - x\htheta}x} \paren{2\sumi x_i^2}^{-1} \paren{-2\paren{y_i - x_i\htheta}x_i}\\
&= \frac{2\paren{\paren{y - x\htheta}x}\paren{\paren{y_i - x_i\htheta}x_i}}{\sumi x_i^2}
\end{align}

シミュレーション

Influence Functionが特定できたので、後はLOOで求めた予測誤差の差分をInfluence Functionでうまく近似できるのかをシミュレーションで確認します。

まずはシミュレーションデータを生成します。
できるだけ単純なデータにしたいので、以下のような特徴量が1つの設定を考えます。
\begin{align}
y &= x + u,\\
x &\sim \mathcal{N}(0, 1),\\
u &\sim \mathcal{N}(0, 0.1^2)
\end{align}

def generate_simulation_data(
    n_incetances: int,
) -> tuple[np.ndarray, np.ndarray]:
    """シミュレーションデータを生成する"""
    x = np.random.normal(0, 1, n_incetances)
    u = np.random.normal(0, 0.1, n_incetances)

    y = x + u

    return (x, y)


x, y = generate_simulation_data(n_incetances=100)

シミュレーションデータに対して、LOOによる予測誤差の変化を計算します。

def estimate_theta(x: np.ndarray, y: np.ndarray) -> float:
    """単回帰モデルの係数を推定する"""

    return (x @ y) / (x @ x)


def calc_leave_one_out_error(x: np.ndarray, y: np.ndarray) -> np.ndarray:
    """LOOでの予測誤差の差分を計算する"""
    
    # ベースラインの全データを用いた学習
    n_incetances = x.shape[0]
    theta_hat = estimate_theta(x, y)
    
    # インスタンスのをひとつずつ取り除いて学習
    error = np.zeros((n_incetances, n_incetances))
    for i in range(n_incetances):
        x_loo = np.delete(x, i, 0)
        y_loo = np.delete(y, i, 0)

        theta_hat_loo = estimate_theta(x_loo, y_loo)
        error[i, :] = (y - x * theta_hat_loo) ** 2 - (y - x * theta_hat) ** 2

    return error


looe = calc_leave_one_out_error(x, y)||<

次に、Influence Functionを用いた近似を行います。
>|python|
def calc_influence(
    x: np.ndarray, y: np.ndarray, x_train: np.ndarray, y_train: np.ndarray
) -> np.ndarray:
    """influenceによる近似"""
    
    # 単回帰の係数
    theta_hat = estimate_theta(x_train, y_train)
    
    # パーツごとに計算
    R2 = 2 * (x_train @ x_train)
    L_train = -2 * (y_train - x_train * theta_hat) * x_train
    L = -2 * (y - x * theta_hat) * x

    return L.reshape(-1, 1) @ L_train.reshape(1, -1) / R2


influence = calc_influence(x, y, x, y)

最後に、LOOとInfluenceを比較します。

def draw_scatter_with_line(x: np.ndarray, y: np.ndarray) -> None:
    """LOOとInfluenceの結果を比較する"""
    
    xx = np.linspace(x.min(), x.max())
    
    fig, ax = plt.subplots()
    ax.plot(xx, xx, c='.7', linewidth=2, zorder=1)
    ax.scatter(x, y, zorder=2)
    ax.set(xlabel="Influence", ylabel="LOO")
    fig.suptitle("InfluenceとLOOの比較")
    fig.savefig(f"output/compare.png")
    fig.show()
    
draw_scatter_with_line(influence.flatten(), looe.flatten())

f:id:dropout009:20210719224841p:plain

ひとつひとつのデータ点が、インスタンス $i$ を取り除いた際のインスタンス $j$ に対する予測誤差の変化を表しています。
点はほぼ $y = x$ 上の線の上に乗っているので、LOOの結果をInfluence Functionでうまく近似できていることがわかります。

まとめ

この記事では、インスタンス重要度を計算するための手法として、LOOによる正確な計算とInfluence Functionによる近似を紹介しました。

インスタンスの重要度を知ることでモデルの振る舞いをより深く理解することができるだけでなく、モデルのデバッグなどに利用することもできる
LOOは正確な反面、計算に時間がかる。Influenceは計算コストを抑えられるが、あくまでも近似であることに注意が必要。特に、モデルが複雑になると近似の精度が下がる可能性がある
LOOはどんなモデルに対しても適用できるが、Influenceはパラメトリックなモデルに対してのみ適用できる。つまり、線形回帰モデルやNeural Netには適用できるが、Random ForestやGradient Boosting Decision Treeには適用できない

最後に、この記事で使ったコードは以下のgithubにアップロードしています。
github.com

参考文献

Koh, Pang Wei, and Percy Liang. "Understanding black-box predictions via influence functions." International Conference on Machine Learning. PMLR, 2017.
Molnar, Christoph. "Interpretable machine learning. A Guide for Making Black Box Models Explainable." (2019). https://christophm.github.io/interpretable-ml-book/.
Hansen, Bruce E. "Econometrics." (2021). https://www.ssc.wisc.edu/~bhansen/econometrics/.

*1:特徴量に注目した機械学習の解釈手法については、拙著「機械学習を解釈する技術」で詳しく説明しています（宣伝）。

機械学習を解釈する技術〜予測力と説明力を両立する実践テクニック

作者:森下光之助
技術評論社

Amazon

*2:モデルが線形回帰で損失が二乗誤差だとこれを満たしますが、Neural Netなどより複雑なモデルだと条件を満たさない可能性はあります。その場合、パラメータが局所最適解に落ちて近似があんまりうまくいかない可能性があります。

*3:本当のことを言うと、線形回帰モデルは再学習無しで正確なインスタンスの重要度を計算することができます。詳細はHansen(2021)をご確認ください

2019-11-20

SHAP(SHapley Additive exPlanations)で機械学習モデルを解釈する

SHapley Additive exPlanations SHAP Random Forest Python interpretable machine learning ゲーム理論 shapley value 機械学習

はじめに
この記事で書いていること、書いていないこと
アルバイトゲームとShapley Value
機械学習モデルへの応用
参考文献

はじめに

ブラックボックスモデルを解釈する手法として、協力ゲーム理論のShapley Valueを応用したSHAP(SHapley Additive exPlanations)が非常に注目されています。SHAPは各インスタンスの予測値の解釈に使えるだけでなく、Partial Dependence Plotのように予測値と変数の関係をみることができ、さらに変数重要度としても解釈が可能であるなど、ミクロ的な解釈からマクロ的な解釈までを一貫して行える点で非常に優れた解釈手法です。

SHAPの論文の作者によって使いやすいPythonパッケージが開発されていることもあり、実際にパッケージを使った実用例はたくさん見かけるので、本記事では協力ゲーム理論の具体例、Shapley Valueのコンセプトと求め方、機械学習モデルを解釈するためのShapley Valueの使われ方を意識してまとめました。

※この記事をベースに2020年1月16日に行われたData Gateway Talk vol.5にて発表した資料は以下になります
speakerdeck.com

※この記事で紹介するSHAPを含んだ、機械学習の解釈手法に関する本を書きました！

機械学習を解釈する技術〜予測力と説明力を両立する実践テクニック

作者:森下光之助
技術評論社

Amazon

この記事で書いていること、書いていないこと

書いていること

協力ゲーム理論の具体例とShapley Valueのコンセプトと求め方
機械学習モデルを解釈するためのShapley Valueの使われ方
shapパッケージの簡単な使い方

書いていないこと

一般的な協力ゲーム理論の概念
Shapley Valueの数学的な性質
実際にShapley Valueを計算するためのアルゴリズム

アルバイトゲームとShapley Value

ここでは協力ゲーム理論のアルバイトゲームを例にとって、Shapley Valueを直感的に理解することを目指します。

まずはアルバイトゲームについて説明します。*1
アルバイトは単独で行うこともできますし、他の人とチームを組んでやってもいいとします。

まずは、1人で働いた場合は、A君が1人でやると6万円、B君が1人でやると4万円、C君が1人でやると2万円がもらえるとしましょう。
次に、2人で働いた場合は、A君とB君が2人でやったときは合計で20万円、A君とC君が2人でやったときは合計で15万円、B君とC君が2人でやったときは合計で10万円がもらえるとしましょう。
最後に、A君B君C君の3人で働いた場合は、合計で24万円がもらえるとしましょう。

これをまとめると以下の表のようになります。

参加者	報酬
A君	6
B君	4
C君	2
A君B君	20
A君C君	15
B君C君	10
A君B君C君	24

今、A君B君C君の3人全員で働いて得た報酬24万円をどうやって分配するのが尤もらしいかを考えます。
直感的には、より貢献度の高い人による多くの報酬を分配するのがフェアな分配のひとつになりそうです。*2
とすると、問題は各人の貢献度をどうやって計るのかということになります。ここで限界貢献度という概念を導入しましょう。これは「各人がアルバイトに参加したときに追加的にどのくらい報酬が増えるか」で計算されます。
たとえば、A君について考えると、限界貢献度は以下のように計算されます。

「誰もいない」→「A君のみ」だと6 - 0 = 6万円
「B君のみ」→「A君とB君」だと20 - 4 = 16万円
「C君のみ」→「A君とC君」だと15 - 2 = 13万円
「B君とC君」→「A君とB君とC君」だと24 - 10 = 14万円

ここでわかるのは、A君の限界報酬はA君が参加する順番に依存するということです。
この影響を打ち消すため、考えられる全ての参加順を用いて平均的な限界貢献度を求めることにしましょう。
発生し得る参加順と、その場合の各人の限界貢献度は以下のようにまとめられます。

参加順	A君の限界貢献度	B君の限界貢献度	C君の限界貢献度
A君→B君→C君	6	14	4
A君→C君→B君	6	9	9
B君→A君→C君	16	4	4
B君→C君→A君	14	4	6
C君→A君→B君	13	9	2
C君→B君→A君	14	8	2

参加順は3!=6通りなので、

A君の平均的な限界貢献度は(6 + 6 + 16 + 14 + 13 + 14) / 6 = 11.5万円
B君の平均的な限界貢献度は(14 + 9 + 4 + 4 + 9 + 8) / 6 = 8万円
C君の平均的な限界貢献度は(4 + 9 + 4 + 6 + 2 + 2) / 6 = 4.5万円

この平均的な限界貢献度のことをShapley Valueと言い、このShapley Valueを用いて報酬を分配しよう、というのがある意味で尤もらしい分配の方法になります。実際、11.5 + 8 + 4.5 = 24万円できれいに分配ができていますし、より貢献度が高い人により多くの報酬が渡るという意味でフェアな分配にもなっています。*3

今回はゲームのプレイヤーがA君B君C君3人のケースを考えました。より一般的なケースとして $N$ 人のプレイヤー $\mathcal{N} = \{1, 2, \dots, N\}$ がゲームに参加するケースを考えると、プレイヤー $i$ のShapley Value $\phi_i$ は以下で計算できます。

\begin{align*}
\phi_i =
\sum_{\mathcal{S} \subset\mathcal{N} \setminus \{i\}}
\frac{S!(N - S - 1)!}{N!}
\bigg(v(\mathcal{S}\cup \{i\}) - v(\mathcal{S})\bigg)
\end{align*}

ここで、 $\mathcal{S}$ は $\mathcal{N}$ からプレイヤー $i$ を除いたプレイヤーの組み合わせです。たとえばA君B君C君3人のケースで、A君のShapley Valueを考える場合は、 $\{\emptyset\}, \{B\}, \{C\}, \{B, C\}$ が該当します。
$S$ は $\mathcal{S}$ の要素の数、つまりプレイヤーの数になります。先程の例だと、それぞれ0人, 1人, 1人, 2人となります。
$v(\cdot)$ は効用を表す関数です。なので、 $v(\mathcal{S}\cup \{i\}) - v(\mathcal{S})$ はプレイヤー $i$ が参加しているときと参加していないときでの効用の差となります。つまり、プレイヤー $i$ が参加したときの限界貢献度となります。

まとめると、プレイヤー $i$ が参加することの限界貢献度を出現する全ての組合わせで求めて平均しています。これはアルバイトゲームの具体例でやったことと全く同じ操作をしています。上式だけみると何を計算しているかよくわからないのですが、具体例をいれて確かめてみると何をやっているかわかりやすいんじゃないかと思います。

機械学習モデルへの応用

最近、協力ゲーム理論のShapley Valueを機械学習モデルの予測結果を解釈するために利用しよう、という研究が発達してきました。
これらの研究では、モデルに投入したひとつひとつの特徴量をゲームのプレイヤーと見立てて、各特徴量の予測への貢献度をShapley Valueで測ろう、ということをやっています。
具体的なシチュエーションを考えてみましょう。今、特徴量として $\mathbf{X} = (X_1, X_2, X_3)$ の3つがあるとします。
モデルを $f(\cdot)$ とすると、平均的な予測値は $E[f( \mathbf{X})$ ]となります。
ここで、ひとつのインスタンスを取り出すと、それぞれ $\mathbf{x} = (x_1, x_2, x_3)$ という値をとっているとします。このとき、予測値としては $f(\mathbf{x})$ が出力されます。

この、平均的な予測値 $E[f( \mathbf{X})$ ]と各インスタンスの予測値 $f(\mathbf{x})$ の乖離に対して、各特徴量がどのくらい影響しているのかを調べます。

各インスタンスの予測値 $f(\mathbf{x})$ は
\begin{align*}
E[f( \mathbf{X} | X_1 = x_1, X_2 = x_2, X_3 = x_3)] & = f( x_1, x_2, x_3 ) = f(\mathbf{x})
\end{align*}
なので、平均的な予測値 $E[f( \mathbf{X})$ ]から $X_1, X_2, X_3$ を条件付けていくことで、その特徴量を知ることが各インスタンスの予測に対してどのように影響するかを知ることができます。具体的に、 $X_1, X_2, X_3$ の順で条件づけていくとすると、たとえば下図のような推移が見られます。

f:id:dropout009:20191117175258p:plain

ここで、 $\phi_j, j = 1, 2, 3$ を各特徴量が予測値に与える限界的な効果としています。（なお、 $\phi_0$ は0と平均的な予測値の乖離で、特に重要ではありません。）

まず、特に何の情報もないところから $X_1 = x_1$ という情報を得ると、予測値が $\phi_1$ だけ大きくなります。さらにその状態から $X_2 = x_2$ という情報を得ると、予測値がさらに $\phi_2$ だけ大きくなります。最後に、 $X_3 = x_3$ という情報を得ると、予測値が $\phi_3$ だけ小さくなって、これが最終的なこのインスタンスへの予測結果となります。

ここで、先程のアルバイトゲームとの共通点が現れています。

各特徴量を一つずつ条件付けていくことで予測値に与える限界的な効果を見ていますが、これはアルバイトゲームで言うところの限界貢献度に対応しています。
また、今回は $X_1, X_2, X_3$ の順で条件づけていますが、当然別の順番で条件づけていくと予測値に与える限界的な効果は変化します。よって、考えうる全ての順序で限界効果を計算し、それを平均しなければなりません。この平均的な限界効果がShapley Valueに対応します。

詳細は論文をご確認頂きたいのですが、このようにShapley Valueを用いて計算された貢献度は、Shapley Valueが持つ望ましい性質を満たすことが証明されています。
ただ、Shapley Valueを計算するのは非常に計算コストがかかるので、実際の計算ではアルゴリズムごとの近似手法が用いられています。特に、tree系のアルゴリズムに対してはTreeSAHPという高速なアルゴリズムが提案されています。

機械学習モデルに対するShapley Valueを簡単で高速に計算できるPythonパッケージにSHAPがあります。

まずは必要なパッケージを読み込みましょう。

import numpy as np
import pandas as pd

# モデルはRandom Forestを使う
from sklearn.ensemble import RandomForestRegressor

# SHAP(SHapley Additive exPlanations)
import shap
shap.initjs() # いくつかの可視化で必要

データはshapパッケージにあるボストンの不動産価格のデータを用います。
データセットの細かい説明はリンクをご確認下さい。

X, y = shap.datasets.boston()
X.head()

f:id:dropout009:20191117191347p:plain

モデルはRandom Forestを使います。

model = RandomForestRegressor(n_estimators=500, n_jobs=-1)
model.fit(X, y)

ここからがshapの使い方になります。shapにはいくつかのExplainerが用意されていて、まずはExplainerにモデルを渡すします。今回はRandom ForestなのでTreeExplainer()を使います。

explainer = shap.TreeExplainer(model, X)

Explainerにはshap_values()メソッドが用意されています。これにShapley Valueを計算したいインプットの行列を渡すことでShapley Valueを計算できます。shapは高速な計算アルゴリズムが実装されており、特にこのデータセットは500行程度なのですぐに計算は終わりますが、計算コストは依然として高いので大きいデータセットのときは適当にサンプリングして渡す必要があります。

shap_values = explainer.shap_values(X)

まずは一つのインスタンスに対してShapley Valueを確認してみます。これは`force_plot()`を使います。

i = 0
shap.force_plot(explainer.expected_value, shap_values[i,:], X.iloc[i,:])

f:id:dropout009:20191117190407p:plain

basevalueの22.51がが全体平均で、output valueの25.64がこのインスタンスに対する予測値となります。なので、このインスタンスは平均よりも高い値が予測されています。なぜこのような予測になったのかを説明するために、各特徴量がどのくらい大きな因子となっているのかを、Shapley Valueで分解して可視化しています。たとえば、このインスタンスはLSTATが4.98をとっていて、これはこのインスタンスの不動産価格に対して大きなプラスの要因となっています。逆に、RMは6.575となっていて、これはマイナス要因であることも見て取れます。プラスとマイナスを総合するとプラスの方が大きくなっていて、最終的には全体平均より3.13高い予測結果になっていることがわかります。
ちなみにLSTATはその地域に住む低所得層の割合、RMは平均的な部屋の数です。

ひとつひとつのインスタンスでShapley Valueを見ていくことでミクロな分析ができますが、よりマクロな分析として、Shapley Valueを変数ごとに平均して変数重要度のように使うこともできます。
今、データセットのインスタンス数が $N$ とすると、変数 $p = 1, \dots, P$ の変数重要度 $\mathrm{Feature Importance}_p$ は以下で計算します。

\begin{align*}
\mathrm{Feature Importance}_p = \frac{1}{N}\sum_{i = 1}^{N} \left|\phi_p^i \right|
\end{align*}

ただし、 $\phi_p^i$ はインスタンス $i$ での変数 $p$ のShapley Valueです。また、プラスマイナスの影響を無視するために絶対値をとっています。
この変数重要度を簡単に可視化するための関数として、summry_plot()が用意されています。

shap.summary_plot(shap_values, X, plot_type="bar")

f:id:dropout009:20191117190121p:plain

Shapley Valueの意味で、LSTATとRMが非常に重要な変数であることが見て取れます。

plot_type = "bar"とすると棒グラフが出ますが、指定しないと一つ一つのShapley Valueがそのまま打たれます。*4

shap.summary_plot(shap_values, X)

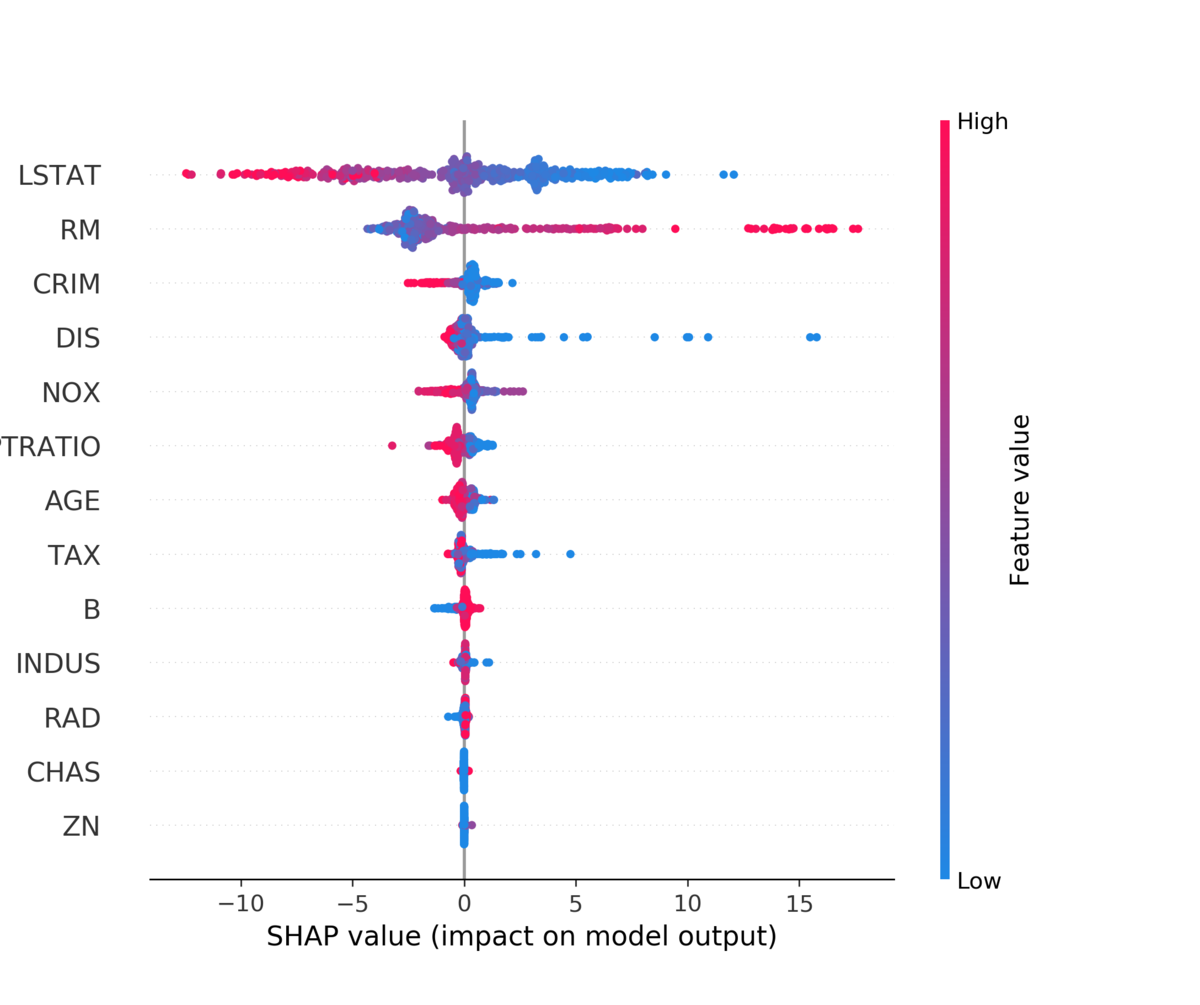
f:id:dropout009:20191117190134p:plain

上に来るほど先程の棒グラフの意味で重要な変数になります。色が赤いほどその変数の値が高いとき、青いほど低いときのShapley Valueになります。Shapley Valueの分布に加えて、LSTATは低いほうがプラスの要因に、RMは高いほうがプラスの要因になりそうなことが見て取れます。

さらに、特徴量の値とShapley Valueの散布図を書くことで、Partial Dependence Plotのような可視化も可能となります。
これは dependence_plot()を使います。今回は特に重要度の高かったLSTATを見てみましょう。

shap.dependence_plot("LSTAT", shap_values, X)

f:id:dropout009:20191117190116p:plain

LSTATの値が大きくなるほどShapley Valueが小さくなることが見て取れます。
色付けは交互作用が見れるように他の変数の値でされています。デフォルトでは交互作用が一番はっきり現れる変数が自動で選ばれます。今回はDISが選ばれていて、DISの値が大きいほど赤く、小さいほど青い点が打たれます。DISはemployment centreからの距離を表しています。グラフの左半分を見ると、同じLSTATの値でもDISが短いほどShapley Valueが高くなる傾向が見て取れます。

参考文献

*1:この数値例は岡田章『新板ゲーム理論』の例をそのままお借りしています。

*2:たとえば、山分けで3等分も考えられますが、この設定ではそれはうまくいきません。A君B君C君の3人で働いて3等分すると報酬は8万円になります。この場合、A君B君だけで働いて報酬を2等分するとA君とB君は10万円を稼ぐことができ、C君を外すインセンティブが生まれてしまいます。

*3:Shapley Valueは数学的に証明された望ましい性質をいくつかもっていますが、ここでは具体例と直感的な性質のみ説明しています。詳細を知りたい場合は協力ゲーム理論の教科書か論文をご確認下さい。

*4:僕はこれの正式な名称を知りません。sina plotでいいのかな？

2019-11-17

tidymodelsとDALEXによるtidyで解釈可能な機械学習

R Random Forest parsnip tidymodels interpretable machine learning ICE PDP 機械学習

はじめに
パッケージ
シミュレーション1
シミュレーション2
- データの作成
- DALEXによる解釈
まとめ
参考文献

※この記事をベースにした2020年1月25日に行われた第83回Japan.Rでの発表資料は以下になります。
speakerdeck.com

※この記事で紹介するSHAPを含んだ、機械学習の解釈手法に関する本を書きました！

機械学習を解釈する技術〜予測力と説明力を両立する実践テクニック

作者:森下光之助
技術評論社

Amazon

はじめに

本記事では、tidymodelsを用いて機械学習モデルを作成し、それをDALEXを用いて解釈する方法をまとめています。
DALEXは

Collection of tools for Visual Exploration, Explanation and Debugging of Predictive Models

を目的とした複数のパッケージから成り立っています。
具体的にどんなパッケージが所属しているかはリンクを確認して下さい。本記事では、特にメインパッケージであるDALEXとingredientsを用います。
ingredientsには、変数重要度、Partial Dependence Plot(PDP)、Individual Conditional Expectation(ICE)、Accumulated Local Effect(ALE)など、特徴量とターゲット変数の関係を見るための関数が用意されています。

なお、本記事ではtidymodelsの使い方には触れないので、過去の記事を参考にして頂ければと思います。

dropout009.hatenablog.com
dropout009.hatenablog.com
dropout009.hatenablog.com

また、本記事では解釈手法そのものには詳しく触れません。Permutationベースの変数重要度やPDP, ICEの詳細な説明は以下の記事も参考にして頂ければと思います。
dropout009.hatenablog.com

パッケージ

本記事で用いるパッケージは以下になります。

library(tidymodels)
library(DALEX) #解釈
library(ingredients) #解釈

library(distributions3) #シミュレーション用
library(colorblindr) #可視化用

set.seed(42)

また、可視化用に以下の関数を用意しておきます

# visualization -----------------------------------------------------------
# ggplot2テーマ
theme_scatter = function() {
  theme_minimal(base_size = 12) %+replace%
    theme(panel.grid.minor = element_blank(),
          panel.grid.major = element_line(color = "gray", size = 0.1),
          legend.position = "top",
          axis.title = element_text(size = 15, color = "black"),
          axis.title.x = element_text(margin = margin(10, 0, 0, 0), hjust = 1),
          axis.title.y = element_text(margin = margin(0, 10, 0, 0), angle = 90, hjust = 1),
          axis.text = element_text(size = 12, color = "black"),
          strip.text = element_text(size = 15, color = "black", margin = margin(5, 5, 5, 5)),
          plot.title = element_text(size = 15, color = "black", margin = margin(0, 0, 18, 0)))
}

シミュレーション1

データ

PDPとICEの関係を浮き彫りにするため、今回はシミュレーションデータを用意します。

特徴量として $X_1, X_2, X_3$ の3つが観測されていいて、
$X_2$ は $X_1$ より強く $Y$ と関係しているが、 $X_3$ は関係してないという状況を考えます。
できるだけ簡単なほうが結果がわかりやすいと思うので、以下の線形で加法な形に特定します。*1

\begin{align}
Y &= X_1 - 5X_2 + \epsilon, \\
X_1, X_2, X_3 &\sim U(-1, 1),\\
\epsilon &\sim \mathcal{N}(0, 0.1^2)
\end{align}

ここで、 $X_1, X_2, X_3$ はそれぞれ独立に区間 $[0, 1$ ]に一様分布し、 $Y$ には平均0で標準偏差0.1の正規分布に従うノイズが乗るとしています。

シミュレーションのために乱数を発生させます。
Rには確率分布を扱うための関数がデフォルトで用意されていますが、distributions3を用いると、より直感的に確率分布を扱うことができます。

N = 1000 #サンプルサイズ

U = Uniform(-1, 1) # 分布を指定
Z = Normal(mu = 0, sigma = 0.1)

X1 = random(U, N) # 分布から乱数を生成
X2 = random(U, N)
X3 = random(U, N)
E = random(Z, N)

Y = X1 - 5*X2 + E 

df = tibble(Y, X1, X2, X3) # データフレームに

データを可視化して $X$ と $Y$ の関係を確認しておきましょう。

df %>% 
  sample_n(200) %>% 
  pivot_longer(cols = contains("X"), values_to = "X") %>% 
  ggplot(aes(X, Y)) +
  geom_point(size = 3, 
             shape = 21,
             color = "white", fill = palette_OkabeIto[5], 
             alpha = 0.7) +
  facet_wrap(~name) + 
  theme_scatter()

f:id:dropout009:20191116212342p:plain

$Y$ は $X_1$ とは弱い正の関係が、 $X_2$ とは強い負の関係があること、 $X_3$ とは無相関であることが見て取れます。

モデル

データの準備ができたので、モデルを作成します。
モデルはtidymodelsの parsnipを使って作成します。

ブラックボックスモデルとして、Random Forestを使うことにします。

fitted = rand_forest(mode = "regression", 
                     trees = 1000,
                     mtry = 3,
                     min_n = 1) %>% 
  set_engine(engine = "ranger", 
             num.threads = parallel::detectCores(), 
             seed = 42) %>% 
  fit(Y ~ ., data = df)

rand_forest()でモデルにRandom Forestを利用することと、そのハイパーパラメータを指定
set_engin()で利用パッケージとパッケージ固有のパラメータを指定
fit()でデータを指定して学習

までを一気に行っています。

DALEXによる解釈

モデルの学習が終わったので、DALEXを用いてモデルの振る舞いを解釈していきましょう。
DALEXによる解釈は、DALEX::explain()でexplainerオブジェクトを作るところから始まります。
嬉しいことに、parsnipで学習したモデルはexplain()にそのまま与えることができます。

> explainer = explain(fitted,# 学習済みモデル
+                     data = df %>% select(-Y), # インプット
+                     y = df %>% pull(Y),# ターゲット
+                     label = "Random Forest")# ラベルをつけておくことができる（なくてもいい）

Preparation of a new explainer is initiated
  -> model label       :  Random Forest 
  -> data              :  1000  rows  3  cols 
  -> data              :  tibbble converted into a data.frame 
  -> target variable   :  1000  values 
  -> predict function  :  yhat.model_fit  will be used (default)
  -> predicted values  :  numerical, min =  -5.886102 , mean =  0.008677733 , max =  5.799964  
  -> residual function :  difference between y and yhat (default)
  -> residuals         :  numerical, min =  -0.1736233 , mean =  -8.650032e-05 , max =  0.1944877  
A new explainer has been created!

あとはexplainerにingredientsで用意された様々な解釈手法を適応するだけです。

変数重要度

まずは変数重要度を見てみましょう。これはexplainerをingredients::feature_importance()に与えるだけで計算できます。

> fi = feature_importance(explainer, 
+                         loss_function = loss_root_mean_square, # 精度の評価関数
+                         type = "raw") # "ratio"にするとフルモデルと比べて何倍悪化するかが出る
> fi
      variable dropout_loss         label
1 _full_model_   0.05063265 Random Forest
2           X3   0.06979976 Random Forest
3           X1   0.80947038 Random Forest
4           X2   4.19405191 Random Forest
5   _baseline_   4.26605636 Random Forest

DALEXは学習アルゴリズムに依存しない手法がベースになっているので、変数重要度の計算もpermutationベースのものが使われます。
つまり、その変数をシャッフルしてどのくらい予測精度が落ちるのかがその変数の重要度として定義とされています。
なお、ingredientsによって作成されたオブジェクトはplot()で簡単に可視化することができます。ggplot2がベースになっているので、ggplot2の設定やレイヤーを+で重ねていくこともできます。

plot(fi)

f:id:dropout009:20191116221221p:plain

変数重要度を見ると、 $X_2$ の重要度が一番高く、 $X_1$ は想定的に重要度が低く、 $X_3$ は全く重要ではないとしていることがわかります。これはそもそものシミュレーションの設定に沿っています。

PDP

次はPDPを見てみましょう。PDPはモデルの平均的な予測結果を可視化したものです。
これもexplainerをingredients::partial_dependency()に与えるだけで計算できます。

pdp = partial_dependency(explainer)

pdp %>% 
  plot() + # ggplot2のレイヤーや設定を重ねていくことができる
  scale_y_continuous(breaks = seq(-6, 6, 2)) + 
  theme_scatter() +
  theme(legend.position = "none")

f:id:dropout009:20191116221810p:plain

モデルが $X_1, X_2, X_3$ と $Y$ の関係をうまく捉えられていることが見て取れます。

シミュレーション2

データの作成

PDPは交互作用がない場合はうまくモデルを解釈する事ができますが、交互作用がある場合は可視化がうまく機能しないことが知られています。
以下のようなシミュレーションを考えてみましょう。

\begin{align}
Y &= X_1 - 5X_2 + 10X_2X_3 + \epsilon, \\
X_1, X_2 &\sim U(-1, 1),\\
X_1, X_2 &\sim Bernoulli(0.5),\\
\epsilon &\sim \mathcal{N}(0, 0.1^2)
\end{align}

今回、 $X_3 = 0$ は0か1をとる変数で、それ単体では効果はありませんが、 $X_2$ との交互作用があり、 $X_2$ は $X_3 = 0$ のときは正の、 $X_3 = 1$ のときは負の効果があるという特定化になっています。

N = 1000

U = Uniform(-1, 1)
B = Bernoulli(p = 0.5)
Z = Normal(mu = 0, sigma = 0.1)

X1 = random(U, N)
X2 = random(U, N)
X3 = random(B, N)
E = random(Z, N)

Y = X1 - 5*X2 + 10*X2*X3 + E

df = tibble(Y, X1, X2, X3)


df %>% 
  sample_n(200) %>% 
  pivot_longer(cols = contains("X"), values_to = "X") %>% 
  ggplot(aes(X, Y)) +
  geom_point(size = 3, 
             shape = 21,
             color = "white", fill = palette_OkabeIto[5], 
             alpha = 0.7) +
  facet_wrap(~name) + 
  theme_scatter()

f:id:dropout009:20191116223552p:plain

DALEXによる解釈

PDP

シミュレーション1と同じくモデルを作成、学習し、explainerオブジェクトを作ります。

fitted = rand_forest(mode = "regression", 
                     trees = 1000,
                     mtry = 3,
                     min_n = 1) %>% 
  set_engine(engine = "ranger", 
             num.threads = parallel::detectCores(), 
             seed = 42) %>% 
  fit(Y ~ ., data = df)


explainer = DALEX::explain(fitted,
                           data = df %>% select(-Y),
                           y = df %>% pull(Y),
                           label = "Random Forest")

PDPも同様に作成します。
このシミュレーションでは $Y$ と $X_2$ の関係をうまく可視化できるかにフォーカスすることにします。

pdp = partial_dependency(explainer, variables = "X2") #変数を限定

pdp %>% 
  plot() + 
  geom_abline(slope = -5, color = "gray70", size = 1) + 
  geom_abline(slope = 5, color = "gray70", size = 1) + 
  scale_y_continuous(breaks = seq(-6, 6, 2),
                     limits = c(-6, 6)) + 
  theme_scatter() +
  theme(legend.position = "none")

f:id:dropout009:20191116230316p:plain
青い線がPDP、グレーの線が本来の関係です。
PDPを見ると、 $X_2$ が動いても予測値にはまるで効果がないように見えます。
念の為ですが、モデルの予測自体はうまくいっています。
Random Forestは交互作用をうまく学習できますし、実際、OOBでの $R^2$ は0.96です。

> fitted
parsnip model object

Fit in:  275msRanger result

Call:
 ranger::ranger(formula = formula, data = data, mtry = ~3, num.trees = ~1000,      min.node.size = ~1, num.threads = ~parallel::detectCores(),      seed = ~42, verbose = FALSE) 

Type:                             Regression 
Number of trees:                  1000 
Sample size:                      1000 
Number of independent variables:  3 
Mtry:                             3 
Target node size:                 1 
Variable importance mode:         none 
Splitrule:                        variance 
OOB prediction error (MSE):       0.3297557 
R squared (OOB):                  0.9624996

ここで起きている現象は、「モデルは交互作用を学習できているが、PDPはそれをうまく可視化できていない」というものです。PDPは交互作用を平均化してしまうため、プラスの交互作用とマイナスの交互作用が相殺して効果がないように見えてしまっています。

ICE Plot

交互作用をうまく捉える手法の一つがICEになります。
ICEは単純にPDPの平均化する前の出力を全てプロットするというものです。
平均化をしていないので交互作用が相殺されることを防ぐことができます。
例によって、ingredients::ceteris_paribus()にexplainerを与えるだけで計算できます。

# 線が多すぎるとわけがわからなくなるので100サンプルだけ抜き出す
# tibbleのまま渡すと警告が出るのでdata.frameにしている。
# 警告の内容を見るとうまく動かなさそうだが、いまのところtibbleのままでもうまく動いているように思う
ice = ceteris_paribus(explainer, 
                      variables = "X2",
                      new_observation = df %>% sample_n(100) %>% as.data.frame()) 

ice %>% 
  plot(alpha = 0.5, size = 0.5, color = colors_discrete_drwhy(1)) + 
  geom_abline(slope = -5, color = "gray70", size = 1) + 
  geom_abline(slope = 5, color = "gray70", size = 1) +
  scale_y_continuous(breaks = seq(-6, 6, 2),
                     limits = c(-6, 6)) + 
  theme_scatter() +
  theme(legend.position = "none")

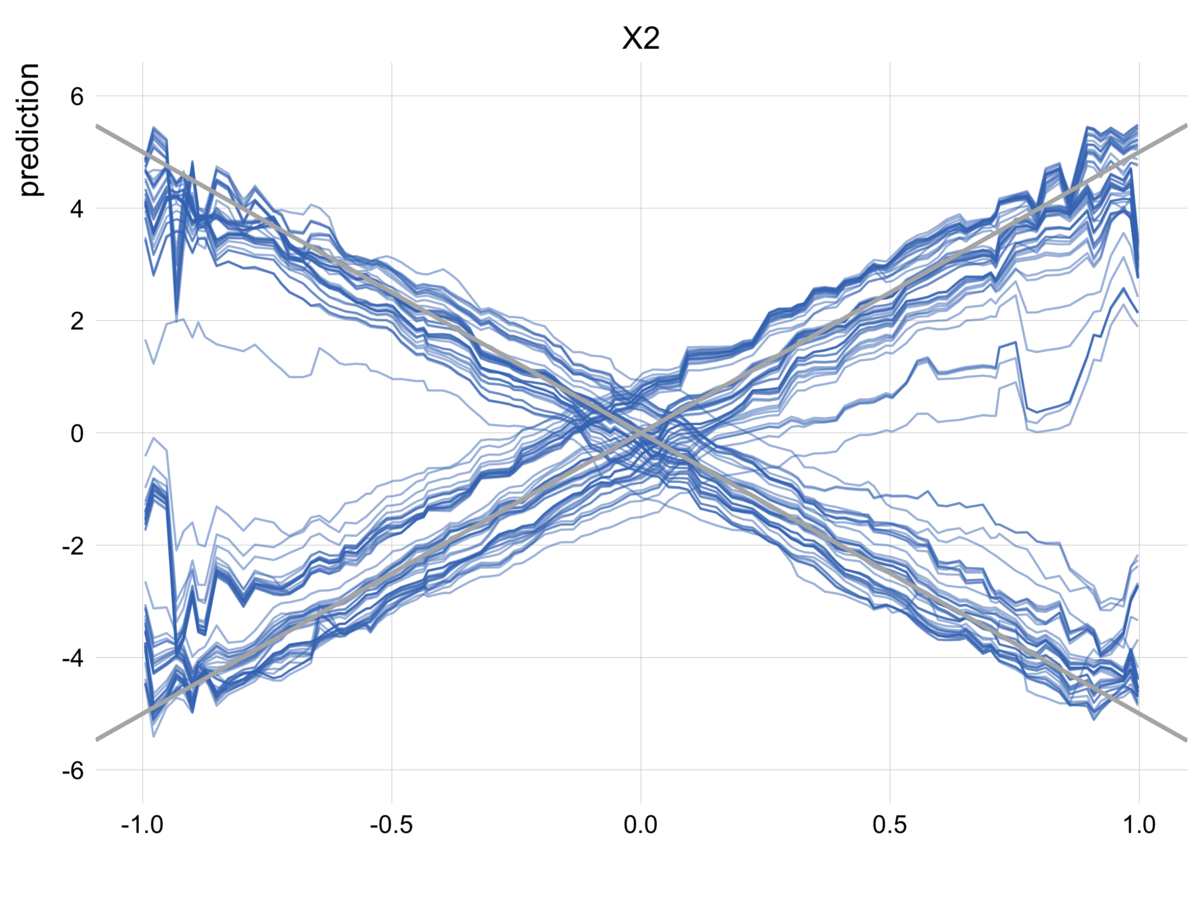
f:id:dropout009:20191116230534p:plain
青い線の一本一本が各インスタンスの予測結果に対応しています。
PDPとは違って、ICEではモデルが交互作用を学習していることをうまく可視化することができています。
なお、各線のタテ方向のブレはインスタンスごとの $X_1$ の大きさによるものです。仮に $X_1$ の値が全てのインスタンスで共通なら一直線上に並んだきれいなX印になります。

Conditional PDP

PDPは交互作用のある変数についても平均化してしまうのが問題でした。
ICEはひとつの解決策でしたが、これはこれでやたら線が多くなってしまいますし、値の安定性も低くなります。
今回は $X_3=0$ のときと $X_3=1$ のときで $X_2$ の効果が逆になることが問題でした。
ということは、 $X_3$ の値でグループに分けてPDPを計算することで、交互作用の問題を解決できそうです。
これを行うための関数がingredients::aggregate_profiles()として用意されています。

# ICEを与える。グループを指定するとPDPをグループごとに求めることができる。
conditional_pdp = aggregate_profiles(ice, groups = "X3") 

conditional_pdp %>% 
  plot() + 
  geom_abline(slope = -5, color = "gray70", size = 1) + 
  geom_abline(slope = 5, color = "gray70", size = 1) +
  scale_y_continuous(breaks = seq(-6, 6, 2),
                     limits = c(-6, 6)) + 
  theme_scatter() +
  theme(legend.position = "none")

f:id:dropout009:20191116232138p:plain

単純なPDPでは捉えられなかった交互作用を可視化することに成功しました。
現実のシチュエーションでは、たとえば男女でグループ分けすることで、モデルが男女の効果の違いを捉えているのかを確認することができます。

clusterd ICE Plot

今回はシミュレーションなので $X_3$ でグループ分けすればいいことがわかっていましたが、実際にはどの変数でグループ化すればいいかわからない場合も多いかと思います。
ingredients::cluster_profiles()を用いることで、似たようなICEをクラスター化してPDPを計算してくれます。

# ICEを与える。クラスター数を指定する。
clustered_ice = cluster_profiles(ice, k = 2)

clustered_ice %>% 
  plot() + 
  geom_abline(slope = -5, color = "gray70", size = 1) + 
  geom_abline(slope = 5, color = "gray70", size = 1) +
  scale_y_continuous(breaks = seq(-6, 6, 2),
                     limits = c(-6, 6)) + 
  theme_scatter() +
  theme(legend.position = "none")