tidymodelsとDALEXによるtidyで解釈可能な機械学習
※この記事をベースにした2020年1月25日に行われた第83回Japan.Rでの発表資料は以下になります。
speakerdeck.com
※この記事で紹介するSHAPを含んだ、機械学習の解釈手法に関する本を書きました!
はじめに
本記事では、tidymodelsを用いて機械学習モデルを作成し、それをDALEXを用いて解釈する方法をまとめています。
DALEXは
Collection of tools for Visual Exploration, Explanation and Debugging of Predictive Models
を目的とした複数のパッケージから成り立っています。
具体的にどんなパッケージが所属しているかはリンクを確認して下さい。本記事では、特にメインパッケージであるDALEXとingredientsを用います。
ingredientsには、変数重要度、Partial Dependence Plot(PDP)、Individual Conditional Expectation(ICE)、Accumulated Local Effect(ALE)など、特徴量とターゲット変数の関係を見るための関数が用意されています。
なお、本記事ではtidymodelsの使い方には触れないので、過去の記事を参考にして頂ければと思います。
dropout009.hatenablog.com
dropout009.hatenablog.com
dropout009.hatenablog.com
また、本記事では解釈手法そのものには詳しく触れません。Permutationベースの変数重要度やPDP, ICEの詳細な説明は以下の記事も参考にして頂ければと思います。
dropout009.hatenablog.com
パッケージ
本記事で用いるパッケージは以下になります。
library(tidymodels) library(DALEX) #解釈 library(ingredients) #解釈 library(distributions3) #シミュレーション用 library(colorblindr) #可視化用 set.seed(42)
また、可視化用に以下の関数を用意しておきます
# visualization ----------------------------------------------------------- # ggplot2テーマ theme_scatter = function() { theme_minimal(base_size = 12) %+replace% theme(panel.grid.minor = element_blank(), panel.grid.major = element_line(color = "gray", size = 0.1), legend.position = "top", axis.title = element_text(size = 15, color = "black"), axis.title.x = element_text(margin = margin(10, 0, 0, 0), hjust = 1), axis.title.y = element_text(margin = margin(0, 10, 0, 0), angle = 90, hjust = 1), axis.text = element_text(size = 12, color = "black"), strip.text = element_text(size = 15, color = "black", margin = margin(5, 5, 5, 5)), plot.title = element_text(size = 15, color = "black", margin = margin(0, 0, 18, 0))) }
シミュレーション1
データ
PDPとICEの関係を浮き彫りにするため、今回はシミュレーションデータを用意します。
特徴量としての3つが観測されていいて、
は
より強く
と関係しているが、
は関係してないという状況を考えます。
できるだけ簡単なほうが結果がわかりやすいと思うので、以下の線形で加法な形に特定します。*1
\begin{align}
Y &= X_1 - 5X_2 + \epsilon, \\
X_1, X_2, X_3 &\sim U(-1, 1),\\
\epsilon &\sim \mathcal{N}(0, 0.1^2)
\end{align}
ここで、はそれぞれ独立に区間
]に一様分布し、
には平均0で標準偏差0.1の正規分布に従うノイズが乗るとしています。
シミュレーションのために乱数を発生させます。
Rには確率分布を扱うための関数がデフォルトで用意されていますが、distributions3を用いると、より直感的に確率分布を扱うことができます。
N = 1000 #サンプルサイズ U = Uniform(-1, 1) # 分布を指定 Z = Normal(mu = 0, sigma = 0.1) X1 = random(U, N) # 分布から乱数を生成 X2 = random(U, N) X3 = random(U, N) E = random(Z, N) Y = X1 - 5*X2 + E df = tibble(Y, X1, X2, X3) # データフレームに
データを可視化して と
の関係を確認しておきましょう。
df %>% sample_n(200) %>% pivot_longer(cols = contains("X"), values_to = "X") %>% ggplot(aes(X, Y)) + geom_point(size = 3, shape = 21, color = "white", fill = palette_OkabeIto[5], alpha = 0.7) + facet_wrap(~name) + theme_scatter()

は
とは弱い正の関係が、
とは強い負の関係があること、
とは無相関であることが見て取れます。
モデル
データの準備ができたので、モデルを作成します。
モデルはtidymodelsの parsnipを使って作成します。
ブラックボックスモデルとして、Random Forestを使うことにします。
fitted = rand_forest(mode = "regression", trees = 1000, mtry = 3, min_n = 1) %>% set_engine(engine = "ranger", num.threads = parallel::detectCores(), seed = 42) %>% fit(Y ~ ., data = df)
- rand_forest()でモデルにRandom Forestを利用することと、そのハイパーパラメータを指定
- set_engin()で利用パッケージとパッケージ固有のパラメータを指定
- fit()でデータを指定して学習
までを一気に行っています。
DALEXによる解釈
モデルの学習が終わったので、DALEXを用いてモデルの振る舞いを解釈していきましょう。
DALEXによる解釈は、DALEX::explain()でexplainerオブジェクトを作るところから始まります。
嬉しいことに、parsnipで学習したモデルはexplain()にそのまま与えることができます。
> explainer = explain(fitted,# 学習済みモデル + data = df %>% select(-Y), # インプット + y = df %>% pull(Y),# ターゲット + label = "Random Forest")# ラベルをつけておくことができる(なくてもいい) Preparation of a new explainer is initiated -> model label : Random Forest -> data : 1000 rows 3 cols -> data : tibbble converted into a data.frame -> target variable : 1000 values -> predict function : yhat.model_fit will be used (default) -> predicted values : numerical, min = -5.886102 , mean = 0.008677733 , max = 5.799964 -> residual function : difference between y and yhat (default) -> residuals : numerical, min = -0.1736233 , mean = -8.650032e-05 , max = 0.1944877 A new explainer has been created!
あとはexplainerにingredientsで用意された様々な解釈手法を適応するだけです。
変数重要度
まずは変数重要度を見てみましょう。これはexplainerをingredients::feature_importance()に与えるだけで計算できます。
> fi = feature_importance(explainer, + loss_function = loss_root_mean_square, # 精度の評価関数 + type = "raw") # "ratio"にするとフルモデルと比べて何倍悪化するかが出る > fi variable dropout_loss label 1 _full_model_ 0.05063265 Random Forest 2 X3 0.06979976 Random Forest 3 X1 0.80947038 Random Forest 4 X2 4.19405191 Random Forest 5 _baseline_ 4.26605636 Random Forest
DALEXは学習アルゴリズムに依存しない手法がベースになっているので、変数重要度の計算もpermutationベースのものが使われます。
つまり、その変数をシャッフルしてどのくらい予測精度が落ちるのかがその変数の重要度として定義とされています。
なお、ingredientsによって作成されたオブジェクトはplot()で簡単に可視化することができます。ggplot2がベースになっているので、ggplot2の設定やレイヤーを+で重ねていくこともできます。
plot(fi)

変数重要度を見ると、の重要度が一番高く、
は想定的に重要度が低く、
は全く重要ではないとしていることがわかります。これはそもそものシミュレーションの設定に沿っています。
PDP
次はPDPを見てみましょう。PDPはモデルの平均的な予測結果を可視化したものです。
これもexplainerをingredients::partial_dependency()に与えるだけで計算できます。
pdp = partial_dependency(explainer) pdp %>% plot() + # ggplot2のレイヤーや設定を重ねていくことができる scale_y_continuous(breaks = seq(-6, 6, 2)) + theme_scatter() + theme(legend.position = "none")

モデルがと
の関係をうまく捉えられていることが見て取れます。
シミュレーション2
データの作成
PDPは交互作用がない場合はうまくモデルを解釈する事ができますが、交互作用がある場合は可視化がうまく機能しないことが知られています。
以下のようなシミュレーションを考えてみましょう。
\begin{align}
Y &= X_1 - 5X_2 + 10X_2X_3 + \epsilon, \\
X_1, X_2 &\sim U(-1, 1),\\
X_1, X_2 &\sim Bernoulli(0.5),\\
\epsilon &\sim \mathcal{N}(0, 0.1^2)
\end{align}
今回、は0か1をとる変数で、それ単体では効果はありませんが、
との交互作用があり、
は
のときは正の、
のときは負の効果があるという特定化になっています。
N = 1000 U = Uniform(-1, 1) B = Bernoulli(p = 0.5) Z = Normal(mu = 0, sigma = 0.1) X1 = random(U, N) X2 = random(U, N) X3 = random(B, N) E = random(Z, N) Y = X1 - 5*X2 + 10*X2*X3 + E df = tibble(Y, X1, X2, X3) df %>% sample_n(200) %>% pivot_longer(cols = contains("X"), values_to = "X") %>% ggplot(aes(X, Y)) + geom_point(size = 3, shape = 21, color = "white", fill = palette_OkabeIto[5], alpha = 0.7) + facet_wrap(~name) + theme_scatter()

DALEXによる解釈
PDP
シミュレーション1と同じくモデルを作成、学習し、explainerオブジェクトを作ります。
fitted = rand_forest(mode = "regression", trees = 1000, mtry = 3, min_n = 1) %>% set_engine(engine = "ranger", num.threads = parallel::detectCores(), seed = 42) %>% fit(Y ~ ., data = df) explainer = DALEX::explain(fitted, data = df %>% select(-Y), y = df %>% pull(Y), label = "Random Forest")
PDPも同様に作成します。
このシミュレーションではと
の関係をうまく可視化できるかにフォーカスすることにします。
pdp = partial_dependency(explainer, variables = "X2") #変数を限定 pdp %>% plot() + geom_abline(slope = -5, color = "gray70", size = 1) + geom_abline(slope = 5, color = "gray70", size = 1) + scale_y_continuous(breaks = seq(-6, 6, 2), limits = c(-6, 6)) + theme_scatter() + theme(legend.position = "none")

青い線がPDP、グレーの線が本来の関係です。
PDPを見ると、が動いても予測値にはまるで効果がないように見えます。
念の為ですが、モデルの予測自体はうまくいっています。
Random Forestは交互作用をうまく学習できますし、実際、OOBでのは0.96です。
> fitted parsnip model object Fit in: 275msRanger result Call: ranger::ranger(formula = formula, data = data, mtry = ~3, num.trees = ~1000, min.node.size = ~1, num.threads = ~parallel::detectCores(), seed = ~42, verbose = FALSE) Type: Regression Number of trees: 1000 Sample size: 1000 Number of independent variables: 3 Mtry: 3 Target node size: 1 Variable importance mode: none Splitrule: variance OOB prediction error (MSE): 0.3297557 R squared (OOB): 0.9624996
ここで起きている現象は、「モデルは交互作用を学習できているが、PDPはそれをうまく可視化できていない」というものです。PDPは交互作用を平均化してしまうため、プラスの交互作用とマイナスの交互作用が相殺して効果がないように見えてしまっています。
ICE Plot
交互作用をうまく捉える手法の一つがICEになります。
ICEは単純にPDPの平均化する前の出力を全てプロットするというものです。
平均化をしていないので交互作用が相殺されることを防ぐことができます。
例によって、ingredients::ceteris_paribus()にexplainerを与えるだけで計算できます。
# 線が多すぎるとわけがわからなくなるので100サンプルだけ抜き出す # tibbleのまま渡すと警告が出るのでdata.frameにしている。 # 警告の内容を見るとうまく動かなさそうだが、いまのところtibbleのままでもうまく動いているように思う ice = ceteris_paribus(explainer, variables = "X2", new_observation = df %>% sample_n(100) %>% as.data.frame()) ice %>% plot(alpha = 0.5, size = 0.5, color = colors_discrete_drwhy(1)) + geom_abline(slope = -5, color = "gray70", size = 1) + geom_abline(slope = 5, color = "gray70", size = 1) + scale_y_continuous(breaks = seq(-6, 6, 2), limits = c(-6, 6)) + theme_scatter() + theme(legend.position = "none")
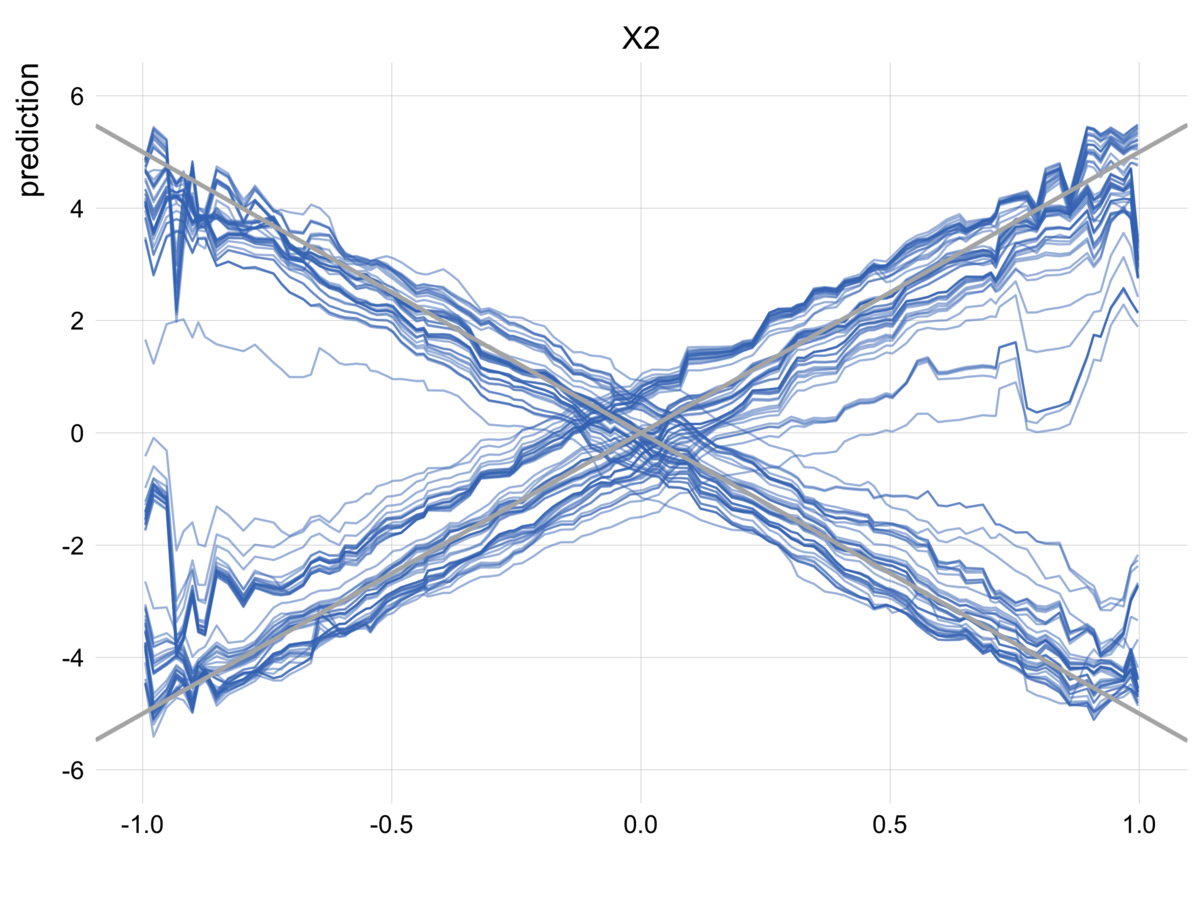
青い線の一本一本が各インスタンスの予測結果に対応しています。
PDPとは違って、ICEではモデルが交互作用を学習していることをうまく可視化することができています。
なお、各線のタテ方向のブレはインスタンスごとのの大きさによるものです。仮に
の値が全てのインスタンスで共通なら一直線上に並んだきれいなX印になります。
Conditional PDP
PDPは交互作用のある変数についても平均化してしまうのが問題でした。
ICEはひとつの解決策でしたが、これはこれでやたら線が多くなってしまいますし、値の安定性も低くなります。
今回はのときと
のときで
の効果が逆になることが問題でした。
ということは、の値でグループに分けてPDPを計算することで、交互作用の問題を解決できそうです。
これを行うための関数がingredients::aggregate_profiles()として用意されています。
# ICEを与える。グループを指定するとPDPをグループごとに求めることができる。 conditional_pdp = aggregate_profiles(ice, groups = "X3") conditional_pdp %>% plot() + geom_abline(slope = -5, color = "gray70", size = 1) + geom_abline(slope = 5, color = "gray70", size = 1) + scale_y_continuous(breaks = seq(-6, 6, 2), limits = c(-6, 6)) + theme_scatter() + theme(legend.position = "none")

単純なPDPでは捉えられなかった交互作用を可視化することに成功しました。
現実のシチュエーションでは、たとえば男女でグループ分けすることで、モデルが男女の効果の違いを捉えているのかを確認することができます。
clusterd ICE Plot
今回はシミュレーションなのででグループ分けすればいいことがわかっていましたが、実際にはどの変数でグループ化すればいいかわからない場合も多いかと思います。
ingredients::cluster_profiles()を用いることで、似たようなICEをクラスター化してPDPを計算してくれます。
# ICEを与える。クラスター数を指定する。 clustered_ice = cluster_profiles(ice, k = 2) clustered_ice %>% plot() + geom_abline(slope = -5, color = "gray70", size = 1) + geom_abline(slope = 5, color = "gray70", size = 1) + scale_y_continuous(breaks = seq(-6, 6, 2), limits = c(-6, 6)) + theme_scatter() + theme(legend.position = "none")

自分ででグループ化した場合と同じく、単純なPDPでは捉えられなかった交互作用を可視化することに成功しました。
まとめ
本記事では、tidymodelsを用いて機械学習モデルを作成し、それをDALEXとingredientsを用いて解釈する方法をまとめました。
もう一つの重要なパッケージであるiBreakDownは別の記事でまとめたいと思っています。
本記事で使用したコードは以下にまとめてあります。
参考文献
- 5.1 Partial Dependence Plot (PDP) | Interpretable Machine Learning
- 5.2 Individual Conditional Expectation (ICE) | Interpretable Machine Learning
- Effects and Importances of Model Ingredients • ingredients
- https://pbiecek.github.io/PM_VEE/
- Causal Interpretations of Black-Box Models
- Peeking Inside the Black Box: Visualizing Statistical Learning with Plots of Individual Conditional Expectation
- Modeling Heterogeneity in Mode-Switching Behavior Under a Mobility-on-Demand Transit System: An Interpretable Machine Learning Approach
*1:実際にこのデータに遭遇したら線形回帰を使ったほうがいいというのはありますが、わかりやすさのためこうしました
