tidymodelsによるtidyな機械学習（その3：ハイパーパラメータのチューニング）

はじめに

前回の記事ではハイパーパラメータのチューニングをfor loopを用いたgrid searchでやっっていました。 tidymodels配下のdialsとtuneを用いることで、より簡単にハイパーパラメータのサーチを行えるので、本記事ではその使い方を紹介したいと思います。 なお、パラメータサーチ以外のtidymodelsの使い方には本記事では言及しないので、以下の記事を参考にして頂ければと思います。

dropout009.hatenablog.com

dropout009.hatenablog.com

前処理

まずは前回の記事と同様、rsampleで訓練/テストデータの分割を行います。なお、例によってデータはdiamondsを用います。

# パッケージ
library(tidyverse)
library(tidymodels)
set.seed(42)

# Train/Testの分割
df_split = initial_split(diamonds,  p = 0.8)

df_train = training(df_split)
df_test  = testing(df_split)

ハイパーパラメータのサーチ

最終的にはtune::tune_grid()でハイパーパラメータを探索しますが、 そのためにTrain/Validationに分割されたデータ、前処理レシピ、学習用モデル、ハイパーパラメータの候補の4つが必要になります。 最初の3つは以前の記事で触れているので、4つ目のハイパーパラメータに関する部分に詳しく触れていきます。

Train/Validationデータ

これはrsamplesの仕事です。普通はCross Validationで評価するので、それに合わせます。

>df_cv = vfold_cv(df_train, v = 5)

> df_cv
#  5-fold cross-validation 
# A tibble: 5 x 2
  splits               id   
  <named list>         <chr>
1 <split [34.5K/8.6K]> Fold1
2 <split [34.5K/8.6K]> Fold2
3 <split [34.5K/8.6K]> Fold3
4 <split [34.5K/8.6K]> Fold4
5 <split [34.5K/8.6K]> Fold5

前処理レシピ

次に、前処理のレシピを作成します。モデルはRandom Forestを使うので、前回の分析同様、前処理は最低限にしておきます。

> rec = recipe(price ~ ., data = df_train) %>% 
+   step_log(price) %>% 
+   step_ordinalscore(all_nominal())
> 
> rec
Data Recipe

Inputs:

      role #variables
   outcome          1
 predictor          9

Operations:

Log transformation on price
Scoring for all_nominal

学習用モデル

parsnipでモデルを設定します。今回もRandom Forestを使いましょう。

> model = rand_forest(mode = "regression",
+                     trees = 50, # 速度重視
+                     min_n = tune(),
+                     mtry = tune()) %>%
+   set_engine("ranger", num.threads = parallel::detectCores(), seed = 42)
> 
> model
Random Forest Model Specification (regression)

Main Arguments:
  mtry = tune()
  trees = 50
  min_n = tune()

Engine-Specific Arguments:
  num.threads = parallel::detectCores()
  seed = 42

Computational engine: ranger 

サーチしたいパラメータはここでは値を決めずtune::tune()を与えます。今回はmin_nとmtryをサーチすることにします。

ハイパーパラメータ

ここが本記事での新しい内容になります。 dialesにはparsnipで指定できるハイパーパラメータに関して、探索するレンジを指定するための関数が用意されています。 たとえばmin_n()はRandom Forestのハイパーパラメータmin_nに対応する関数で、デフォルトだと2-40のレンジでハイパーパラメータが探索されます。 なお、これは最終ノードに最低でも必要なインスタンスの数を表していて、これを大きくするとより強い正則化がかかります。

> min_n()
Minimal Node Size  (quantitative)
Range: [2, 40]

自分でレンジを決めたい場合は引数で指定することができます。

> min_n(range = c(1, 10))
Minimal Node Size  (quantitative)
Range: [1, 10]

同様に、もうひとつのハイパーパラメータmtryに関しても見てみましょう。 こちらは各ツリーでの分割の際に用いる特徴量の数で、これを小さくするとより強い正則化がかかります。

> mtry()
# Randomly Selected Predictors  (quantitative)
Range: [1, ?]

min_n()とは違って、レンジの最大値が指定されていません。モデルに投入する特徴量の数よりも大きいmtryを探索しても意味がない*1ので、こちらで直接指定してあげる必要があります。 この際、mtry(range = c(1, 5))のようにレンジを指定することもできますが、実際にモデルに投入するデータフレームを与えてあげることでレンジを指定することもできます。

> # 前処理済み学習用データ
> df_input = rec %>% 
+   prep() %>% 
+   juice() %>% 
+   select(-price)
> 
> finalize(mtry(), df_input)
# Randomly Selected Predictors  (quantitative)
Range: [1, 9]

dials::finalize()の第1引数にレンジを指定したい関数を、第2引数に特徴量のデータフレームを指定することで、適切なレンジが指定されます。 特徴量の数は分析の途中で変動するので、このやり方は柔軟性があって良いんじゃないかと思います。

さて、これで探索範囲の指定ができるようになりました。 次に、探索したいハイパーパラメータのリストを作ってtune::parameters()に与えるとparametersオブジェクトを作ることができます。

> params = list(min_n(),
+               mtry() %>% finalize(rec %>% prep() %>% juice() %>% select(-price))) %>% 
+   parameters()
> 
> params
Collection of 2 parameters for tuning

    id parameter type object class
 min_n          min_n    nparam[+]
  mtry           mtry    nparam[+]

このparametersオブジェクトをdials::grid_*()に渡すことで、実際に探索するハイパーパラメータの値を作ることができます。 たとえばgrid_regular()ならグリッドサーチ、grid_random()ならランダムサーチになります。 今回はランダムサーチにしましょう。サーチの数はsizeで指定できます。

> df_grid = params %>% 
+   grid_random(size = 10) # 実際はもっと多いほうがいい
> 
> df_grid
# A tibble: 10 x 2
   min_n  mtry
   <int> <int>
 1     7     8
 2    19     8
 3    22     3
 4    38     1
 5    12     8
 6    36     1
 7    21     6
 8     7     5
 9    29     2
10    38     3

チューニング

これでハイパーパラメータの探索準備が整いました！ これまでに作ったオブジェクトをtune::tune_grid()に渡します。

df_tuned = tune_grid(object = rec,
                     model = model, 
                     resamples = df_cv,
                     grid = df_grid,
                     metrics = metric_set(rmse, mae, rsq),
                     control = control_grid(verbose = T))

• object：recipeで作成された前処理レシピを渡します。resamplesに与えたデータがこの前処理を済ませたあとでモデルに投入されます。
• model：parsnipで定義した学習用のモデルです。
• resamples：rsamplesで作った学習/評価用のデータを渡します。普通はCross Varidationで評価すると思うのでrsamples::vfold_cv()で作ったデータフレームを渡すのがいいと思います。
• grid：dialsとtuneで作ったハイパーパラメータの候補が格納されたデータフレームを渡します。
• metrics：精度の評価指標です。yardsticに準備されている関数を指定することができます。
• control：指定しなくても構いませんが、今回はログが出力されるようにしています。

学習/評価が終わると、以下のようなデータフレームが手に入ります。

> df_tuned
#  5-fold cross-validation 
# A tibble: 5 x 4
  splits               id    .metrics          .notes          
* <list>               <chr> <list>            <list>          
1 <split [34.5K/8.6K]> Fold1 <tibble [20 × 5]> <tibble [0 × 1]>
2 <split [34.5K/8.6K]> Fold2 <tibble [20 × 5]> <tibble [0 × 1]>
3 <split [34.5K/8.6K]> Fold3 <tibble [20 × 5]> <tibble [0 × 1]>
4 <split [34.5K/8.6K]> Fold4 <tibble [20 × 5]> <tibble [0 × 1]>
5 <split [34.5K/8.6K]> Fold5 <tibble [20 × 5]> <tibble [0 × 1]>

.metricsに予測精度が格納されています。unnest()でもとってこれますが、手っ取り早い関数としてtune::collect_metrics()が準備されています。

> df_tuned %>% 
+   collect_metrics()
# A tibble: 30 x 7
    mtry min_n .metric .estimator   mean     n  std_err
   <int> <int> <chr>   <chr>       <dbl> <int>    <dbl>
 1     1    38 mae     standard   0.120      5 0.00131 
 2     1    38 rmse    standard   0.159      5 0.00173 
 3     1    38 rsq     standard   0.979      5 0.000246
 4     2    29 mae     standard   0.0792     5 0.000317
 5     2    29 rmse    standard   0.107      5 0.000518
 6     2    29 rsq     standard   0.989      5 0.000160
 7     4    19 mae     standard   0.0677     5 0.000174
 8     4    19 rmse    standard   0.0932     5 0.000441
 9     4    19 rsq     standard   0.992      5 0.000109
10     5     3 mae     standard   0.0651     5 0.000176
# … with 20 more rows

特に精度の高いハイパーパラメータの候補が知りたい場合は、tune::show_best()で確認することができます。

> df_tuned %>% 
+   show_best(metric = "rmse", n_top = 3, maximize = FALSE)
# A tibble: 3 x 7
   mtry min_n .metric .estimator   mean     n  std_err
  <int> <int> <chr>   <chr>       <dbl> <int>    <dbl>
1     7     8 rmse    standard   0.0910     5 0.000702
2     5     3 rmse    standard   0.0912     5 0.000558
3     7    16 rmse    standard   0.0915     5 0.000679

一番精度の高かったハイパーパラメータを使って全訓練データでモデルを再学習する場合は、tune::select_best()でハイパーパラメータをとってきてupdate()でモデルをアップデートできます。

# 一番精度の良かったハイパーパラメータ
> df_best_param = df_tuned %>% 
+   select_best(metric = "rmse", maximize = FALSE)
> df_best_param
# A tibble: 1 x 2
   mtry min_n
  <int> <int>
1     7     8

# モデルのハイパーパラメータを更新
> model_best = update(model, df_best_param)
> model_best
Random Forest Model Specification (regression)

Main Arguments:
  mtry = 7
  trees = 50
  min_n = 8

Engine-Specific Arguments:
  num.threads = parallel::detectCores()
  seed = 42

Computational engine: ranger 

あとは通常通り学習・評価を行うだけです。

まとめ

本記事ではtidymodels配下のdialsとtuneを用いたハイパーパラメータのサーチを紹介しました。 前回の記事ではCross Validationデータにどうアクセスするか結構ややこしかったと思うのですが、tuneを用いることでよりスッキリと探索と評価を行うことができます。 dialsとtuneは公式ドキュメントに個別の使い方はまとまっているのですが、目的がわかりにくい部分や、どの情報が最新かわからないところもあり、典型的なタスクに対しての用途を自分でまとめ直したという経緯になります。

ちなみに、今回はランダムサーチを用いましたが、tuneではbaysian optimizationを用いたパラメータ探索も可能となっています。ぜひ確認してみて下さい*2

本記事で使用したコードは以下にまとめてあります。

github.com

参考文献

• Tools for Creating Tuning Parameter Values • dials
• Tidy Tuning Tools • tune

*1:実際は特徴量の数よりも大きい値を入れるとエラーを吐きます

*2:Classification Example • tune

Synthetic Difference In Differences(Arkhangelsky et. al., 2019)を読んだ

はじめに

GW中にSynthetic difference in differences(Arkhangelsky, D., Athey, S., Hirshberg, D. A., Imbens, G. W., & Wager, S. (2019)) を読みました。
ランダム化比較試験（RCT）が行えない状況でのパネルデータのから処置効果を推定する際には、バイアスを取り除くためにDifference In DifferencesやSynthetic Controlがよく用いられていますが、
Synthetic Difference In Differencesは名前の通りDifference In DifferencesとSynthetic Controlのいいとこ取りになっています。
パネルデータから因果推論を行う際に非常に強力な武器になると思ったので、本記事でコンセプトをまとめ、論文内の比較実験を再現しました。

コンセプト

セッティング

のユニット（たとえば個人）に対して時点でのデータがとれているパネルデータを考えます。このとき、アウトカムは以下の行列で表現できます。*1

\begin{align}
\mathbf{Y}
= \begin{pmatrix}
Y_{11} & \cdots & Y_{1T}\\
\vdots & \ddots & \vdots\\
Y_{N1} & \cdots & Y_{NT}
\end{pmatrix}
\end{align}

簡単のために、一番シンプルな設定として、のユニットが 時点のみ処置を受けるケースを考えます。つまり、 はコントロール群(c)では処置群(t)になりますし、が処置前(pre)、が処置後(post)となります。

ここで、仮想的にのユニットが時点で処置を受けた場合のアウトカムを、受けなかった場合のアウトカムをと書くことにしましょう。このとき、つまり処置を受けた場合と受けなかった場合の差をみることで、処置がアウトカムに与えるインパクトを測定することができます。ただ、実際に僕たちに観測できるのは処置を受けたのみで、処置を受けなかったときのは観測することができません。そこで、なんらかの手法を使って、実際には観測できないを推定する必要が出てきます。これを反事実と呼びます。以降、反事実を推定する手法としてDifference In DIfference(DID)、Synthetic Control(SC)、そしてその融合であるSynthetic Difference In Difference(SDID)を比較していきます。

Difference in Differences (DID)

処置前コントロール群の値にに加えて、(1)コントロール群と処置群のアウトカムにそもそもどのくらい違いがあるのか、(2)処置を受けなくても処置の前後でどのくらいアウトカムが変わるのかを考慮することで、処置後処置群の値が推定できるのではというのがDIDの発想です。具体的には、DIDによる推定量は以下で定義されます。

\begin{align}
\hat{Y}_{NT}^{\text{DID}}(0) &= \bar{Y}^{c, pre} + \left(\bar{Y}^{c, post} - \bar{Y}^{c, pre}\right)+ \left(\bar{Y}^{t, pre} - \bar{Y}^{c, pre}\right)\\
&=\frac{1}{N- 1}\frac{1}{T-1}\sum_{i=1}^{N-1}\sum_{t=1}^{T-1}Y_{it} \\
&\quad+ \left(\frac{1}{N- 1}\sum_{i=1}^{N-1}Y_{iT} - \frac{1}{N- 1}\frac{1}{T-1}\sum_{i=1}^{N-1}\sum_{t=1}^{T-1}Y_{it}\right)\\
&\quad+ \left(\frac{1}{T-1}\sum_{t=1}^{T-1}Y_{Nt} - \frac{1}{N- 1}\frac{1}{T-1}\sum_{i=1}^{N-1}\sum_{t=1}^{T-1}Y_{it}\right)
\end{align}

ここで、はそれぞれのグループの平均値を表しています。上式は以下のように解釈できます。まず、単に処置前コントロール群のみを用いて予測を行うと（第一項）、コントロール群と処置群の違いでバイアスがかかり、次に処置前と処置後の違いでもバイアスがかかります。そこで、コントロール群<->処置群の差を第二項で、処置前<->処置後の差を第三項で補正しています。この意味において、DID推定量はバイアスを二重に補正していると言えます。

最後に、こうしてDIDで推定したと実際の観測値の差を見ることで処置のインパクトが推定できます。

\begin{align}
\hat{\tau}^{\text{DID}} = Y_{NT}(1) -\hat{Y}_{NT}^{\text{DID}}(0)
\end{align}

Synthetic Control (SC)

DIDは単純平均でしたが、コントロール群の加重平均で処置群を表現しようというのがSCの発想になります。SCは以下の2ステップを踏みます。まず、加重平均に用いる各コントロール群の重みを、うまく処置群を近似できるように決めます。

\begin{align}
\sum_{i=1}^{N-1} \hat{\omega}_{i} Y_{it} \approx Y_{N t} \text { for all } t=1, \ldots, T-1
\end{align}

具体的には、以下の二乗誤差を小さくするようにを求めます。

\begin{align}
\hat{\omega}&=\underset{\omega \in \mathbb{W}}{\arg \min }\;\frac{1}{T-1} \sum_{t=1}^{T-1}\left(\sum_{i=1}^{N-1} \omega_{i} Y_{i t}-Y_{N t}\right)^{2} + \frac{1}{2}\zeta\|\omega\|_2\\
\text{where}\quad \mathbb{W}&=\left\{\omega \in \mathbb{R}^{N - 1} \;\bigg|\; \omega_{i} \geq 0, \; \sum_{i=1}^{N-1} \omega_{i}=1\right\}
\end{align}

は加重平均の重みなので0以上、足して1の制約がかかっています。また、正則化を入れることでの推定を安定させています。

次に、この重みを使って処置後であるを推定します。
\begin{align}
\hat{Y}_{N T}^{\mathrm{SC}}(0)=\frac{1}{T-1} \sum_{i=1}^{N-1} \sum_{t=1}^{T-1} \hat{\omega}_{i} Y_{i t}+\left(\sum_{i=1}^{N-1} \hat{\omega}_{i}Y_{i T}-\frac{1}{T-1} \sum_{i=1}^{N-1} \sum_{t=1}^{T-1} \hat{\omega}_{i}Y_{i t}\right)
\end{align}

DIDの推定量と見比べると：

• DIDでは単純平均でしたが、SCは加重平均を用いることで処置群の近似を改善しています。
• その一方で、SCにはDIDにあった処置前後のバイアス補正（第三項）が存在しません。

Synthetic Difference In Differences (SDID)

DIDとSCを見比べることで、双方の利点と欠点が見えました。そこで、SDIDでは両方のいいとこ取りをします。つまり、

• 単純平均ではなく加重平均を用いる
• コントロール/トリートメントのバイアス補正だけでなく、処置前後のバイアス補正を入れる

ことで反事実のよりよい推定を目指します。

\begin{align}
\hat{Y}_{N T}^{\mathrm{SDID}}(0)= \sum_{i=1}^{N-1} \sum_{t=1}^{T-1} \hat{\omega}_{i} \hat{\lambda}_{t} Y_{i t}+\left(\sum_{t=1}^{T-1} \hat{\lambda}_{t}Y_{N t}-\sum_{t=1}^{T-1} \sum_{i=1}^{N-1} \hat{\omega}_{i}\hat{\lambda}_{t} Y_{i t}\right)+\left(\sum_{i=1}^{N-1} \hat{\omega}_{i}Y_{i T}-\sum_{i=1}^{N-1} \sum_{t=1}^{T-1} \hat{\omega}_{i}\hat{\lambda}_{t} Y_{i t}\right)
\end{align}

ここで、は時間方向の重みであり、と同様に以下の最小化問題を解くことで求めます。

\begin{align}
\hat{\lambda}&=\underset{\lambda_0\in\mathbb{R},\; \lambda \in \mathbb{L}}{\arg \min } \;\frac{1}{N-1}\sum_{i=1}^{N-1}\left(\lambda_0 + \sum_{t=1}^{T-1} \lambda_{t} Y_{i t}-Y_{i T}\right)^{2}+ \frac{1}{2}\xi\|\lambda\|_2\\
\text{where}\quad \mathbb{L}&=\left\{\lambda \in \mathbb{R}^{T - 1} \;\bigg|\; \lambda_{t} \geq 0, \; \sum_{t=1}^{T-1} \lambda_{t}=1\right\}
\end{align}

ただし、トレンドに対応するためにが入っています。これは重みとしては用いません。

比較実験

論文ではAbadie, Diamond, and Hainmueller(2010)のデータを用いてDID, SC, SDIDを比較した実験を行っているので、それを再現した結果を紹介します。

ADH(2010)ではカリフォルニアの禁煙法が喫煙に与えたインパクトをSynthetic Controlを用いて推定しています。
使用データはカリフォルニアを含むアメリカ39州の年度別喫煙量のデータで、1970年から2000年にかけて31年分あります。なお、禁煙法は1989年から実施されています。
今回の実験では実際に禁煙法の効果を調べたいのではなく、をうまく予測できるかを確かめたいので、処置前（1988年以前）のデータに関して、各州の1期先の喫煙量を他の38州の喫煙量からDID/SC/SDIDで予測し、精度を検証します。*2
よりよい精度で1期先の予測ができるなら、処置の効果をより正確に推定できると言えます。

具体的には、各州に対して1980年から1988年までの9年分の予測をDID/SC/SDIDで行い、RMSEを計算します。
\begin{align}
\operatorname{RMSE}_{i}=\sqrt{\frac{1}{9} \sum_{t=1980}^{1988}\left(Y_{it}-\hat{Y}_{it}\right)^{2}}
\end{align}

その結果が以下になります。

DID/SCと比較して、SDIDはより高い精度でを予測することに成功しています。中央値で見るとDIDと比較して50%、SCと比較しても15%の改善です。

具体的にどの部分で精度に差が出ているのかプロットを見て確認してみます。

上図は各州の喫煙量の実測値とDID/SC/SDIDの推定値がプロットされています。横軸が年度で縦軸が喫煙量です。
図が細かいのですが、基本的にSDID（赤）はDID（オレンジ）/SC（緑）よりも実測値Y（青）をうまく予測できています。
特に差が顕著な部分をいくつか抜き出したものが下の図になります。

DIDは全体的に精度が悪いと思いますが、
Synthetic Controlは非常に特徴的で、New HampshireやUtahなど、他の州の加重平均で表現できない州は予測がうまくいっていません。
これに対して、SDIDは非常にロバストな予測ができています。

まとめ

本記事では、Difference In DifferencesとSynthetic Controlを融合させたSynthetic Difference In Differencesのコンセプトをまとめ、実際に精度が改善することを確認しました。
SDIDはRCTが行えない状況でパネルデータの因果推論を行う際、非常に強力な武器になると思います。

参考文献

Arkhangelsky, D., Athey, S., Hirshberg, D. A., Imbens, G. W., & Wager, S. (2019). Synthetic difference in differences (No. w25532). National Bureau of Economic Research.[1812.09970] Synthetic Difference in Differences

GitHub - swager/sdid-script: Example scripts for synthetic difference in differences

Alberto Abadie, Alexis Diamond, and Jens Hainmueller. Synthetic control methods for comparative case studies: Estimating the effect of California’s tobacco control program. Journal of the American Statistical Association, 105(490):493–505, 2010.　https://economics.mit.edu/files/11859

再現コード
GitHub - dropout009/sdid_python: replication python code for synthetic difference in difference simulation. please check https://arxiv.org/abs/1812.09970 and https://github.com/swager/sdid-script

*1:簡単のため、とりあえず共変量は無視することにします。

*2:論文ではやってませんが、カリフォルニアを除いてしまえば2000年まで実験することもできると思います

XGBoostの論文を読んだのでGBDTについてまとめた

はじめに

今更ですが、XGboostの論文を読んだので、2章GBDT部分のまとめ記事を書こうと思います。*1
この記事を書くにあたって、できるだけ数式の解釈を書くように心がけました。数式の意味をひとつひとつ追っていくことは、実際にXGBoost（またはLightGBMやCatBoostなどのGBDT実装）を使う際にも役立つと考えています。たとえばハイパーパラメータがどこに効いているかを理解することでチューニングを効率化したり、モデルを理解することでよりモデルに合った特徴量のエンジニアリングができるのではないかと思います。

また、この記事に限りませんが、記述に間違いや不十分な点などあればご指摘頂ければ嬉しいです。

XGBoost論文

目的関数の設定

一般的な状況として、サンプルサイズがで特徴量の数がのデータに対する予測モデルを構築することを想定しましょう。*2
今回はツリーをアンサンブルした予測モデルを構築します。
のツリーを加法的に組み合わせた予測モデルは以下のように定式化できます。*3

\begin{align}
\hat{y}_{i} &= \phi\left(\mathbf{x}_{i}\right)=\sum_{k\in\mathcal{K}} f_{k}\left(\mathbf{x}_{i}\right),\\
\text{where}\quad f_{k} \in \mathcal{F} &= \left\{f(\mathbf{x})=w_{q(\mathbf{x})}\right\}\left(q : \mathbb{R}^{m} \rightarrow \mathcal{T},\; \mathcal{T} = \{1, \dots, T\}, \; w \in \mathbb{R}^{T}\right)
\end{align}

ここで、はひとつひとつのツリーを表しています。ツリーは特徴量 が与えられると、それをに従って各ノードに紐づけ、それぞれのノードに対応する予測値を返します。そして、ひとつひとつのツリーの予測値を足し合わせることで、最終的な予測結果とします。

では、具体的にツリーをどうやって作っていくかを決めるために、最小化したい目的関数を設定します。

\begin{align}
\mathcal{L}(\phi) &= \sum_{i\in \mathcal{I}} l\left(y_{i}, \hat{y}_{i}\right)+\sum_{k\in \mathcal{K}} \Omega\left(f_{k}\right), \\
\text{where}\quad\Omega(f) &= \gamma T+\frac{1}{2} \lambda\|w\|^{2} = \gamma T+\frac{1}{2} \lambda \sum_{t \in \mathcal{T}} w_{t}^{2}
\end{align}

ここで、は損失関数で、たとえば二乗誤差になります。ただし、単に二乗誤差を最小化するのではなく、過適合を回避して汎化性能を上げるために正則化項が追加されています。なお、とはハイパーパラメータであり、交差検証などで最適な値を探索する必要があります。

• の第一項はツリーのノードの数に応じてペナルティが課されるようになっています。ハイパーパラメータを大きくするとよりノード数少ないツリーが好まれるようになります。ツリーの大きさに制限をかけることで過適合を回避することが目的です。
• の第二項は各ノードが返す値の大きさに対してペナルティがかかることを意味しています。ハイパーパラメータを大きくすると、（絶対値で見て）より小さいが好まれるようになります。が小さいということは最終的な出力を決める部分で足し合わされる値が小さくなるので、過適合を避けることに繋がります。

勾配ブースティング

さて、目的関数を最小化するような個のツリー構築したいわけですが、個ツリーを同時に構築して最適化するのではなく、個目のツリーを作る際には、個目までに構築したツリーを所与として、目的関数を最小化するようなツリーを作ることにしましょう。*4

\begin{align}
\min_{f_k}\;\mathcal{L}^{(k)}=\sum_{i\in\mathcal{I}} l\left(y_{i}, \hat{y}_i^{(k - 1)}+f_{k}\left(\mathbf{x}_{i}\right)\right)+\Omega\left(f_{k}\right)
\end{align}

このステップで作成する個目のツリーを合わせた予測値はであり、個目までのツリーではうまく予測できていない部分に対してフィットするように新しいツリーを構築すると解釈できます。このように残差に対してフィットするツリーを逐次的に作成していく手法をブースティングと呼びます。

さて、損失関数を直接最適化するのではなく、その2階近似を最適化することにしましょう。後にわかるように、2次近似によって解析的に解を求めることができます。の周りで2階のテイラー展開を行うと、目的関数は以下で近似できます。

\begin{align}
\mathcal{L}^{(k)} &\approx \sum_{i\in\mathcal{I}}\left[l\left(y_{i}, \hat{y}^{(k - 1)}\right)+g_{i} f_{k}\left(\mathbf{x}_{i}\right)+\frac{1}{2} h_{i} f_{k}^{2}\left(\mathbf{x}_{i}\right)\right] + \Omega\left(f_{k}\right),\\
\text{where} \quad g_i &= \frac{\partial }{\partial \hat{y}^{(k - 1)}}l\left(y_{i}, \hat{y}^{(k - 1)}\right),\\
h_i &= \frac{\partial^2 }{\partial \left(\hat{y}^{(k - 1)}\right)^2}l\left(y_{i}, \hat{y}^{(k - 1)}\right)
\end{align}

ここで、とはそれぞれ損失関数の1階と2階の勾配情報になります。勾配情報を使ったブースティングなので勾配ブースティングと呼ばれています。*5
今回を動かすことで目的関数を最小化するので、と関係ない第一項は無視できます。

\begin{align}
\tilde{\mathcal{L}}^{(k)} &=\sum_{i\in\mathcal{I}}\left[g_{i} f_{k}\left(\mathbf{x}_{i}\right)+\frac{1}{2} h_{i} f_{k}^{2}\left(\mathbf{x}_{i}\right)\right]+\gamma T+\frac{1}{2} \lambda \sum_{t \in \mathcal{T}} w_{t}^{2} \\
&= \sum_{t \in \mathcal{T}}\left[\sum_{i \in \mathcal{I}_{t}} g_{i} f_{k}\left(\mathbf{x}_{i}\right)+\frac{1}{2} \sum_{i \in \mathcal{I}_{t}} h_{i} f_{k}^{2}\left(\mathbf{x}_{i}\right)\right]+\gamma T +\frac{1}{2} \lambda \sum_{t \in \mathcal{T}} w_{t}^{2}\\
&=\sum_{t \in \mathcal{T}}\left[\left(\sum_{i \in \mathcal{I}_{t}} g_{i}\right) w_{t}+\frac{1}{2}\left(\lambda + \sum_{i \in \mathcal{I}_{t}} h_{i}\right) w_{t}^{2}\right]+\gamma T
\end{align}

• 1行目の式では、と関係ない第一項を取り除き、の中身を書き下しました。
• 2行目への変換ですが、全てのについて足し合わせている部分を、まずノードに所属する部分を足し合わせてから、全てのノードについて足し合わせるように分解しています。
• 3行目への変換では、同じノードに所属するは全てを返すというツリーの性質を利用しています。また、の共通部分をくくっています。

さて、はに関しての2次式なので、解析的に解くことができます。

\begin{align}
w_{t}^{*}=-\frac{\sum_{i \in \mathcal{I}_{t}} g_{i}}{\lambda + \sum_{i \in \mathcal{I}_{t}} h_{i}}
\end{align}

以上で、個目のツリーに関して、各ノードが返すべき値が解析的に求まりました。*6
この式からもハイパーパラメータを大きくするとが（絶対値で見て）小さくなることが見て取れます。このを元の目的関数に代入してあげることで

\begin{align}
\tilde{\mathcal{L}}^{(k)}(q)=-\frac{1}{2} \sum_{t\in\mathcal{T}} \frac{\left(\sum_{i \in \mathcal{I}_{t}} g_{i}\right)^2}{\lambda + \sum_{i \in \mathcal{I}_{t}} h_{i}}+\gamma T
\end{align}

を得ます。あとはツリーの構造、言い換えれば特徴量の分割ルールを決める必要があります。たとえば、一番シンプルなケースとして、全く分割を行わない場合（）と一度だけ分割を行う場合（に分割）を比較しましょう。分割による目的関数の値の減少分は

\begin{align}
\mathcal{L}_{\text{split}}&= -\frac{1}{2} \frac{\left(\sum_{i \in \mathcal{I}} g_{i}\right)^2}{\lambda + \sum_{i \in \mathcal{I}} h_{i}}+\gamma - \left(-\frac{1}{2} \frac{\left(\sum_{i \in \mathcal{I}_L} g_{i}\right)^2}{\lambda + \sum_{i \in \mathcal{I}_L} h_{i}}-\frac{1}{2} \frac{\left(\sum_{i \in \mathcal{I}_R} g_{i}\right)^2}{\lambda + \sum_{i \in \mathcal{I}_R} h_{i}}+2\gamma \right)\\
&= \frac{1}{2}\left(\frac{\left(\sum_{i \in \mathcal{I}_L} g_{i}\right)^2}{\lambda + \sum_{i \in \mathcal{I}_L} h_{i}}+\frac{\left(\sum_{i \in \mathcal{I}_R} g_{i}\right)^2}{\lambda + \sum_{i \in \mathcal{I}_R} h_{i}} - \frac{\left(\sum_{i \in \mathcal{I}} g_{i}\right)^2}{\lambda + \sum_{i \in \mathcal{I}} h_{i}}\right) - \gamma
\end{align}

であり、これがプラスなら分割を行い、マイナスなら分割を行わないということになります。上式からも、ハイパーパラメータ を大きくするとより分割が行われなくなることが見て取れます。

ところで、そもそもどの特徴量のどの値で分割するべきかなのでしょうか？一番ナイーブな考え方は、全ての変数に対して全ての分割点を考慮して、一番目的関数の値を減少させるような分割を選ぶというものがあります。ただし、この方法は膨大な計算量が必要になるため、XGBoostでは近似手法が提供されており、3章に記述されています。さらに、4章移行では並列計算や比較実験などが記されています。

まとめ

XGboostの論文を読んだので、自身の理解を深めるために2章GBDT部分のまとめ記事を書きました。
今までなんとなく使っていたハイパーパラメータが具体的にどの部分に効いているのか学ぶことができて、とても有意義だったと感じています。

参考文献

[1603.02754] XGBoost: A Scalable Tree Boosting System
Overview of tree algorithms from decision tree to xgboost
NIPS2017読み会 LightGBM: A Highly Efficient Gradient Boosting Decision T…
XGBoostの概要 - ともにゃん的データ分析ブログ

*1:なお、元論文のノーテーションがおかしい/統一的でないように感じたので、一部表記を変更しています。

*2:元論文ではですが、 とが混じるとややこしい気もするのでにしました。

*3:元論文のとなっているのですが、はインデックスを返す関数なので、タイポかと思われます。

*4:元論文の添字がツリーの数とややこしいのでのまま進めることにしました。

*5:たぶん

*6:論文にはこれがimpuityみたいなものと書かれているのですが、不勉強で理解できませんでした。

tidymodelsによるtidyな機械学習（その2：Cross Varidation）

はじめに

本記事ではtidymodelsを用いたCross Validationとハイパーパラメータのチューニングについて紹介したいと思います。 なお、tidymodelsの基本的な操作方法については以下の記事をご覧下さい。

dropout009.hatenablog.com

前処理

まずは前回の記事と同様、訓練/テストデータの分割と前処理を行います。なお、例によってデータはdiamondsを用います。

# パッケージ
library(tidyverse)
library(tidymodels)
set.seed(42)

# 分割
df_split = initial_split(diamonds,  p = 0.8)

df_train = training(df_split)
df_test  = testing(df_split)

# 前処理レシピ
rec = recipe(price ~ ., data = df_train) %>% 
  step_log(price) %>% 
  step_ordinalscore(all_nominal())

Cross Validation

さて、ここからが新しい内容になります。

df_cv = vfold_cv(df_train, v = 10)

> df_cv
#  10-fold cross-validation 
# A tibble: 10 x 2
   splits               id    
   <list>               <chr> 
 1 <split [38.8K/4.3K]> Fold01
 2 <split [38.8K/4.3K]> Fold02
 3 <split [38.8K/4.3K]> Fold03
 4 <split [38.8K/4.3K]> Fold04
 5 <split [38.8K/4.3K]> Fold05
 6 <split [38.8K/4.3K]> Fold06
 7 <split [38.8K/4.3K]> Fold07
 8 <split [38.8K/4.3K]> Fold08
 9 <split [38.8K/4.3K]> Fold09
10 <split [38.8K/4.3K]> Fold10

tidymodels配下のrsampleパケージにはCross Validationを行うための関数vfold_cv()があるので、これを使います。

> df_cv$splits[[1]]
<38837/4316/43153>

splitsを確認します。全43153サンプルを38837の訓練データと4316の検証データに分割していることを示しています。

> df_cv$splits[[1]] %>% analysis()
# A tibble: 38,837 x 10
   carat cut       color clarity depth table price     x     y     z
   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
 1 0.23  Ideal     E     SI2      61.5    55   326  3.95  3.98  2.43
 2 0.21  Premium   E     SI1      59.8    61   326  3.89  3.84  2.31
 3 0.23  Good      E     VS1      56.9    65   327  4.05  4.07  2.31
 4 0.290 Premium   I     VS2      62.4    58   334  4.2   4.23  2.63
 5 0.31  Good      J     SI2      63.3    58   335  4.34  4.35  2.75
 6 0.24  Very Good J     VVS2     62.8    57   336  3.94  3.96  2.48
 7 0.26  Very Good H     SI1      61.9    55   337  4.07  4.11  2.53
 8 0.22  Fair      E     VS2      65.1    61   337  3.87  3.78  2.49
 9 0.23  Very Good H     VS1      59.4    61   338  4     4.05  2.39
10 0.3   Good      J     SI1      64      55   339  4.25  4.28  2.73

> df_cv$splits[[1]] %>% assessment()
# A tibble: 4,316 x 10
   carat cut       color clarity depth table price     x     y     z
   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
 1  0.24 Very Good I     VVS1     62.3    57   336  3.95  3.98  2.47
 2  0.3  Very Good J     VS2      62.2    57   357  4.28  4.3   2.67
 3  0.23 Very Good F     VS1      59.8    57   402  4.04  4.06  2.42
 4  0.31 Good      H     SI1      64      54   402  4.29  4.31  2.75
 5  0.32 Good      H     SI2      63.1    56   403  4.34  4.37  2.75
 6  0.22 Premium   E     VS2      61.6    58   404  3.93  3.89  2.41
 7  0.3  Very Good I     SI1      63      57   405  4.28  4.32  2.71
 8  0.24 Premium   E     VVS1     60.7    58   553  4.01  4.03  2.44
 9  0.26 Very Good D     VVS2     62.4    54   554  4.08  4.13  2.56
10  0.86 Fair      E     SI2      55.1    69  2757  6.45  6.33  3.52
# ... with 4,306 more rows

訓練データにはanalysis()で、検証データにはassesment()でアクセスできます。

CVデータが準備できたので、学習と予測を行いましょう。まずは適当なRandom Forestモデルを用意します。

rf = rand_forest(mode = "regression",
                 trees = 50,
                 min_n = 10,
                 mtry = 3) %>%
  set_engine("ranger", num.threads = parallel::detectCores(), seed = 42)

CVデータに前処理レシピを適用するにはmap()とprepper()を使います。

> df_cv %>% 
+   mutate(recipes = map(splits, prepper, recipe = rec))
#  10-fold cross-validation 
# A tibble: 10 x 3
   splits               id     recipes     
 * <list>               <chr>  <list>      
 1 <split [38.8K/4.3K]> Fold01 <S3: recipe>
 2 <split [38.8K/4.3K]> Fold02 <S3: recipe>
 3 <split [38.8K/4.3K]> Fold03 <S3: recipe>
 4 <split [38.8K/4.3K]> Fold04 <S3: recipe>
 5 <split [38.8K/4.3K]> Fold05 <S3: recipe>
 6 <split [38.8K/4.3K]> Fold06 <S3: recipe>
 7 <split [38.8K/4.3K]> Fold07 <S3: recipe>
 8 <split [38.8K/4.3K]> Fold08 <S3: recipe>
 9 <split [38.8K/4.3K]> Fold09 <S3: recipe>
10 <split [38.8K/4.3K]> Fold10 <S3: recipe>

prepper()はprep()前のレシピを渡すことで、CV訓練データを用いてprep()したレシピを返してくれます。

次に前処理済みのCVデータでモデルを学習します。

> df_cv %>% 
+   mutate(recipes = map(splits, prepper, recipe = rec),
+          fitted = map(recipes, ~ fit(rf, price ~ ., data = juice(.))))
#  10-fold cross-validation 
# A tibble: 10 x 4
   splits               id     recipes      fitted  
 * <list>               <chr>  <list>       <list>  
 1 <split [38.8K/4.3K]> Fold01 <S3: recipe> <fit[+]>
 2 <split [38.8K/4.3K]> Fold02 <S3: recipe> <fit[+]>
 3 <split [38.8K/4.3K]> Fold03 <S3: recipe> <fit[+]>
 4 <split [38.8K/4.3K]> Fold04 <S3: recipe> <fit[+]>
 5 <split [38.8K/4.3K]> Fold05 <S3: recipe> <fit[+]>
 6 <split [38.8K/4.3K]> Fold06 <S3: recipe> <fit[+]>
 7 <split [38.8K/4.3K]> Fold07 <S3: recipe> <fit[+]>
 8 <split [38.8K/4.3K]> Fold08 <S3: recipe> <fit[+]>
 9 <split [38.8K/4.3K]> Fold09 <S3: recipe> <fit[+]>
10 <split [38.8K/4.3K]> Fold10 <S3: recipe> <fit[+]>

学習モデルを用いて検証用データに対して予測を行います。

# ラッパーを作っておく
pred_wrapper = function(split_obj, rec_obj, model_obj, ...) {
  df_pred = bake(rec_obj, assessment(split_obj)) %>%
    bind_cols(predict(model_obj, .)) %>% 
    select(price, .pred)
  
  return(df_pred)
}

> df_cv %>% 
+   mutate(recipes = map(splits, prepper, recipe = rec),
+          fitted = map(recipes, ~ fit(rf, price ~ ., data = juice(.))),
+          predicted = pmap(list(splits, recipes, fitted), pred_wrapper))
#  10-fold cross-validation 
# A tibble: 10 x 5
   splits               id     recipes      fitted   predicted           
 * <list>               <chr>  <list>       <list>   <list>              
 1 <split [38.8K/4.3K]> Fold01 <S3: recipe> <fit[+]> <tibble [4,316 × 2]>
 2 <split [38.8K/4.3K]> Fold02 <S3: recipe> <fit[+]> <tibble [4,316 × 2]>
 3 <split [38.8K/4.3K]> Fold03 <S3: recipe> <fit[+]> <tibble [4,316 × 2]>
 4 <split [38.8K/4.3K]> Fold04 <S3: recipe> <fit[+]> <tibble [4,315 × 2]>
 5 <split [38.8K/4.3K]> Fold05 <S3: recipe> <fit[+]> <tibble [4,315 × 2]>
 6 <split [38.8K/4.3K]> Fold06 <S3: recipe> <fit[+]> <tibble [4,315 × 2]>
 7 <split [38.8K/4.3K]> Fold07 <S3: recipe> <fit[+]> <tibble [4,315 × 2]>
 8 <split [38.8K/4.3K]> Fold08 <S3: recipe> <fit[+]> <tibble [4,315 × 2]>
 9 <split [38.8K/4.3K]> Fold09 <S3: recipe> <fit[+]> <tibble [4,315 × 2]>
10 <split [38.8K/4.3K]> Fold10 <S3: recipe> <fit[+]> <tibble [4,315 × 2]>

pmap()は入力列が複数の場合のmap()の拡張です。

予測結果を用いて検証用データで精度を計算して完了です。

> df_cv %>% 
+   mutate(recipes = map(splits, prepper, recipe = rec),
+          fitted = map(recipes, ~ fit(rf, price ~ ., data = juice(.))),
+          predicted = pmap(list(splits, recipes, fitted), pred_wrapper),
+          evaluated = map(predicted, metrics, price, .pred))
#  10-fold cross-validation 
# A tibble: 10 x 6
   splits               id     recipes      fitted   predicted            evaluated       
 * <list>               <chr>  <list>       <list>   <list>               <list>          
 1 <split [38.8K/4.3K]> Fold01 <S3: recipe> <fit[+]> <tibble [4,316 × 2]> <tibble [3 × 3]>
 2 <split [38.8K/4.3K]> Fold02 <S3: recipe> <fit[+]> <tibble [4,316 × 2]> <tibble [3 × 3]>
 3 <split [38.8K/4.3K]> Fold03 <S3: recipe> <fit[+]> <tibble [4,316 × 2]> <tibble [3 × 3]>
 4 <split [38.8K/4.3K]> Fold04 <S3: recipe> <fit[+]> <tibble [4,315 × 2]> <tibble [3 × 3]>
 5 <split [38.8K/4.3K]> Fold05 <S3: recipe> <fit[+]> <tibble [4,315 × 2]> <tibble [3 × 3]>
 6 <split [38.8K/4.3K]> Fold06 <S3: recipe> <fit[+]> <tibble [4,315 × 2]> <tibble [3 × 3]>
 7 <split [38.8K/4.3K]> Fold07 <S3: recipe> <fit[+]> <tibble [4,315 × 2]> <tibble [3 × 3]>
 8 <split [38.8K/4.3K]> Fold08 <S3: recipe> <fit[+]> <tibble [4,315 × 2]> <tibble [3 × 3]>
 9 <split [38.8K/4.3K]> Fold09 <S3: recipe> <fit[+]> <tibble [4,315 × 2]> <tibble [3 × 3]>
10 <split [38.8K/4.3K]> Fold10 <S3: recipe> <fit[+]> <tibble [4,315 × 2]> <tibble [3 × 3]>

ハイパーパラメータのサーチ

Cross Validationで精度を計算する方法がわかったので、これを用いてハイパーパラメータのサーチを行います。 今回はmin_nのみグリッドサーチすることにします。

grid_min_n = c(5, 10, 15)
df_result_cv = tibble() # 結果をいれる
for (n in grid_min_n) {
  
  rf = rand_forest(mode = "regression",
                   trees = 50,
                   min_n = n,
                   mtry = 3) %>%
    set_engine("ranger", num.threads = parallel::detectCores(), seed = 42)
  
  tmp_result = df_cv %>% 
    mutate(recipes = map(splits, prepper, recipe = rec),
           fitted = map(recipes, ~ fit(rf, price ~ ., data = juice(.))),
           predicted = pmap(list(splits, recipes, fitted), pred_wrapper),
           evaluated = map(predicted, metrics, price, .pred))
  
  df_result_cv = df_result_cv %>% 
    bind_rows(tmp_result %>% 
                select(id, evaluated) %>% 
                mutate(min_n = n))
}

> df_result_cv %>% 
+   unnest() %>% 
+   group_by(min_n, .metric) %>% 
+   summarise(mean(.estimate))
# A tibble: 9 x 3
# Groups:   min_n [?]
  min_n .metric `mean(.estimate)`
  <dbl> <chr>               <dbl>
1     5 mae                0.0671
2     5 rmse               0.0932
3     5 rsq                0.992 
4    10 mae                0.0679
5    10 rmse               0.0940
6    10 rsq                0.991 
7    15 mae                0.0686
8    15 rmse               0.0947
9    15 rsq                0.991 

どうやらmin_n = 5の精度が最も良さそうです。 このパラメータを用いて訓練データ全体でモデルを再学習し、予測精度を確認します。 parsnipで作ったモデルはupdate()でパラメータを更新できます。

rf_best = update(rf, min_n = 5)

rec_preped = rec %>% 
  prep(df_train)

fitted = rf_best %>% 
  fit(price ~ ., data = juice(rec_preped))


df_test_baked = bake(rec_preped, df_test)


> df_test_baked %>% 
+   bind_cols(predict(fitted, df_test_baked)) %>% 
+   metrics(price, .pred)
# A tibble: 3 x 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 rmse    standard      0.0905
2 rsq     standard      0.992 
3 mae     standard      0.0665

予測結果と実際の値もプロットして確認します。

df_test_baked %>% 
  bind_cols(predict(fitted, df_test_baked)) %>% 
  ggplot(aes(.pred, price)) +
  geom_hex() +
  geom_abline(slope = 1, intercept = 0) + 
  coord_fixed() +
  scale_x_continuous(breaks = seq(6, 10, 1), limits = c(5.8, 10.2)) + 
  scale_y_continuous(breaks = seq(6, 10, 1), limits = c(5.8, 10.2)) + 
  scale_fill_viridis_c() + 
  labs(x = "Prediction", y = "Truth") + 
  theme_minimal(base_size = 12) +
  theme(panel.grid.minor = element_blank(),
        axis.text = element_text(color = "black", size =12))

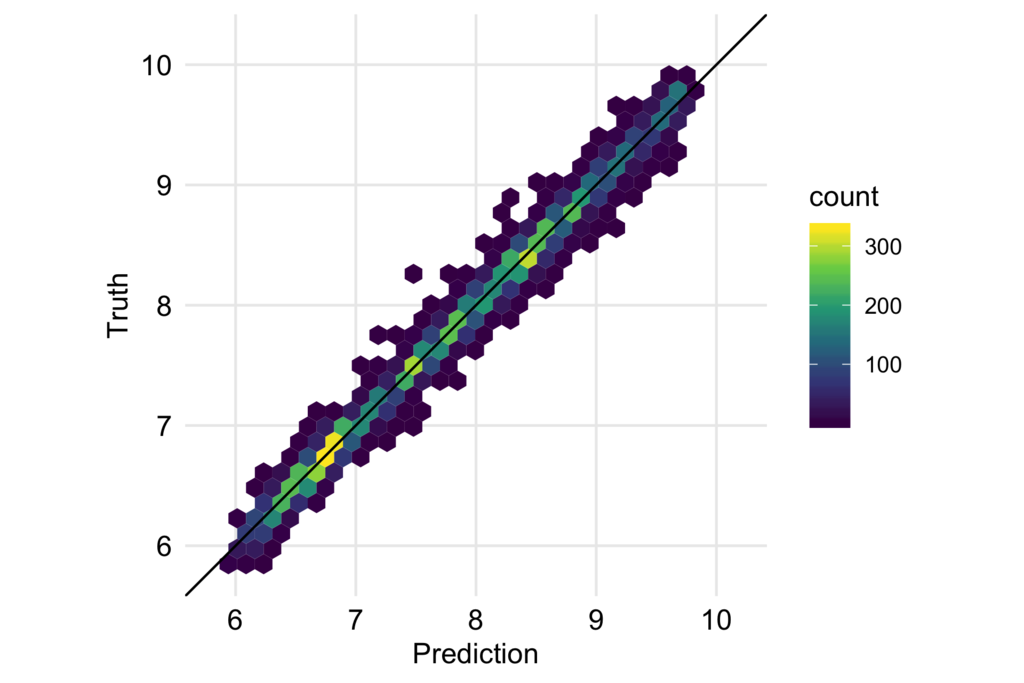
大きく外したり系統的なバイアスも見られないので、うまく予測できていると言えるのではないかと思います。

まとめ

tidymodels配下のパッケージ、特にpurrrとrsampleを用いることでtidyにCross Validationを行うことができました。

参考

• Recipes with rsample • rsample
• Grid Search Tuning of Keras Models • rsample
• Regression Example • parsnip

変数重要度とPartial Dependence Plotで機械学習モデルを解釈する

はじめに

RF/GBDT/NNなどの機械学習モデルは古典的な線形回帰モデルよりも高い予測精度が得られる一方で、インプットとアウトプットの関係がよくわからないという解釈性の問題を抱えています。 この予測精度と解釈性のトレードオフでどちらに重点を置くかは解くべきタスクによって変わってくると思いますが、私が仕事で行うデータ分析はクライアントの意思決定に繋げる必要があり、解釈性に重きを置いていることが多いです。

とはいえ機械学習モデルの高い予測精度は惜しく、悩ましかったのですが、学習アルゴリズムによらずモデルに解釈性を与えられる手法が注目され始めました。 本記事では変数重要度とPDP/ICE Plot (Partial Dependence/Individual Conditional Expectation)を用いて所謂ブラックボックスモデルを解釈する方法を紹介します。

※この記事で紹介する変数重要度やPD/ICEを含んだ、機械学習の解釈手法に関する本を書きました！

機械学習を解釈する技術〜予測力と説明力を両立する実践テクニック

モデルの学習

まずはパッケージを読み込みます。

library(tidyverse)
library(tidymodels)

library(pdp) # partial dependence plot
library(vip) # variable importance plot

例によってdiamondsデータを使用し、Rondom Forestでダイヤの価格を予測するモデルを作ります。 tidymodelsの使い方は以前の記事をご覧下さい。

set.seed(42)

df_split = initial_split(diamonds,  p = 0.9)

df_train = training(df_split)
df_test  = testing(df_split)


rec = recipe(price ~ carat + clarity + color + cut, data = df_train) %>% 
  step_log(price) %>% 
  step_ordinalscore(all_nominal()) %>% 
  prep(df_train)

df_train_baked = juice(rec)
df_test_baked = bake(rec, df_test)

fitted = rand_forest(mode = "regression", 
                     trees = 100,
                     min_n = 5,
                     mtry = 2) %>% 
  set_engine("ranger", num.threads = parallel::detectCores(), seed = 42) %>% 
  fit(price ~ ., data = juice(rec))

> fitted
parsnip model object

Ranger result

Call:
 ranger::ranger(formula = formula, data = data, mtry = ~2, num.trees = ~100,      min.node.size = ~5, num.threads = ~parallel::detectCores(),      seed = ~42, verbose = FALSE) 

Type:                             Regression 
Number of trees:                  100 
Sample size:                      48547 
Number of independent variables:  4 
Mtry:                             2 
Target node size:                 5 
Variable importance mode:         none 
Splitrule:                        variance 
OOB prediction error (MSE):       0.01084834 
R squared (OOB):                  0.9894755 

変数重要度

モデルの解釈において最も重要なのは、どの変数がアウトプットに強く影響し、どの変数は影響しないのかを特定すること、つまり変数重要度を見ることだと思います。 たとえば特に重要な変数を見定めて施策を打つことでアウトプットをより効率よく改善できる可能性が高まりますし*1、ありえない変数の重要度が高く出ていればデータやモデルが間違っていることに気づけるかもしれません。

tree系のアルゴリズムだとSplit（分割の回数）やGain（分割したときの誤差の減少量）などで変数重要度を定義することもできますが、ここではアルゴリズムに依存しない変数重要度であるPermutationベースのものを紹介します。 Permutationベースの変数重要度のコンセプトは極めて直感的で、「ある変数の情報を壊した時にモデルの予測精度がすごく落ちるならそれは大事な変数だ」というものです。

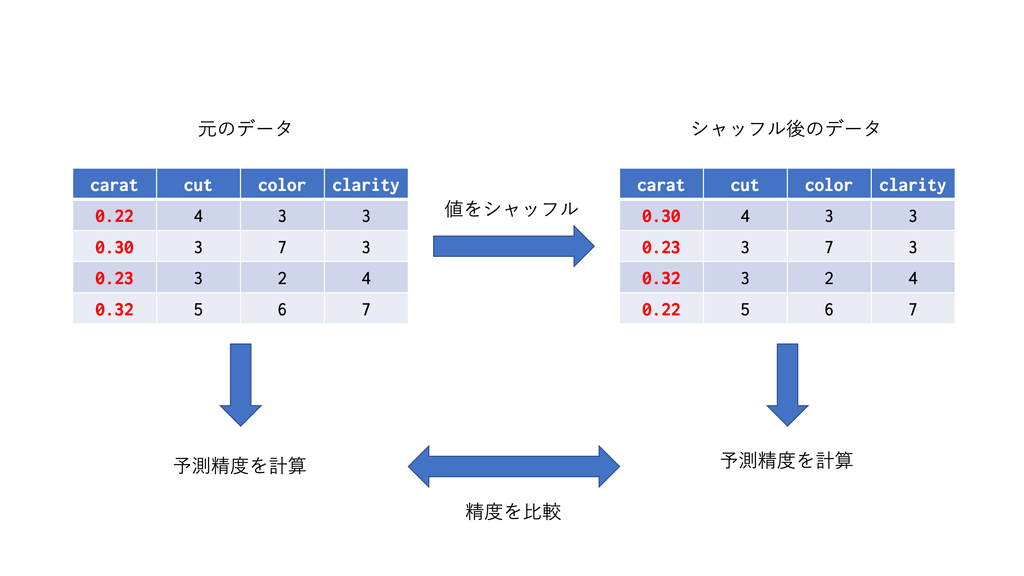
たとえば今回のモデルでcaratの変数重要度を見たいとします。

1. 訓練データを使って学習済みモデルを用意し、テストデータに対する予測精度を出します。
2. テストデータのcarat列の値をシャッフルしますし、シャッフル済みテストデータを使って同様に予測を行います。
3. 2つの予測精度を比較し、予測精度の減少度合いを変数重要度とします。

carat列のシャッフルによって、もしcaratが重要な変数ならモデルは的はずれな予測をするようになりますし、逆に重要でないなら特に影響は出ないはずで、これはある意味においての変数の重要度を捉えらていると思います。

また、この手法はあくまで予測の際に用いるデータをシャッフルしていて、学習をやり直しているわけではないため、計算が軽いことも利点です。

さて、実際にPermutationベースの変数重要度を計算してみましょう。 パッケージはvipを使います。変数重要度が計算できるパッケージは他にもいくつかありますが、vipはPermutationベースの変数重要度が計算でき、次に見るPartial Dependence Plotで利用するパッケージpdpと同じシンタックスが使えます（作者が同じなので）

# objectとnewdataを受けて予測結果をベクトルで返す関数を作っておく必要がある
pred_wrapper = function(object, newdata) {
  return(predict(object, newdata) %>% pull(.pred))
}


fitted %>% 
  vip(method = "permute",  # 変数重要度の計算方法
      pred_fun = pred_wrapper, 
      target = df_test_baked %>% pull(price),
      train = df_test_baked %>% select(-price),
      metric = "rsquared", # 予測精度の評価関数) 

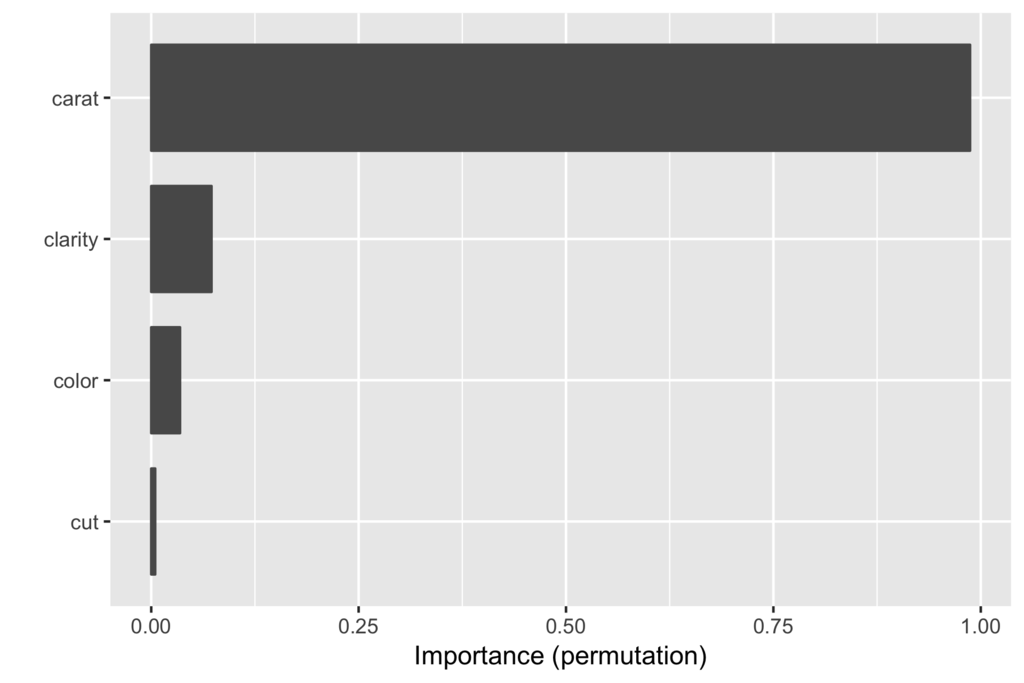
一番手っ取り早い方法はvip()関数を使った可視化です（グラフを自分で細かくいじりたい場合はvi()での計算結果を自分で可視化します）。 caratの変数重要度がその他の変数と比べてダントツであることが見て取れます。

Partial Dependence Plot

各変数の重要度がわかったら、次に行うべきは重要な変数とアウトカムの関係を見ることだと思います。 ただ、一般にブラックボックスモデルにおいてインプットとアウトカムの関係は非常に複雑で、可視化することは困難です。

そこで、複雑な関係を要約する手法の一つにPartial Dependence Plot(PDP)があります。PDPは興味のある変数以外の影響を周辺化して消してしまうことで、インプットとアウトカムの関係を単純化しようというものです。

特徴量を とした学習済みモデル があるとします。 を興味のある変数 とその他の変数 に分割し、以下のpartial dependence function

\begin{align} \hat{f_{s}}(x_s) = E_c\left[ \hat{f}(x_s, x_c) \right] = \int \hat{f}(x_s, x_c) p(x_c) d x_c \end{align}

を定義し、これを

\begin{align} \bar{f_{s}}(x_s) = \frac{1}{N}\sum_i\hat{f}\left(x_s, x_c^{(i)}\right) \end{align}

で推定します。具体的には以下のようなことをやっています。

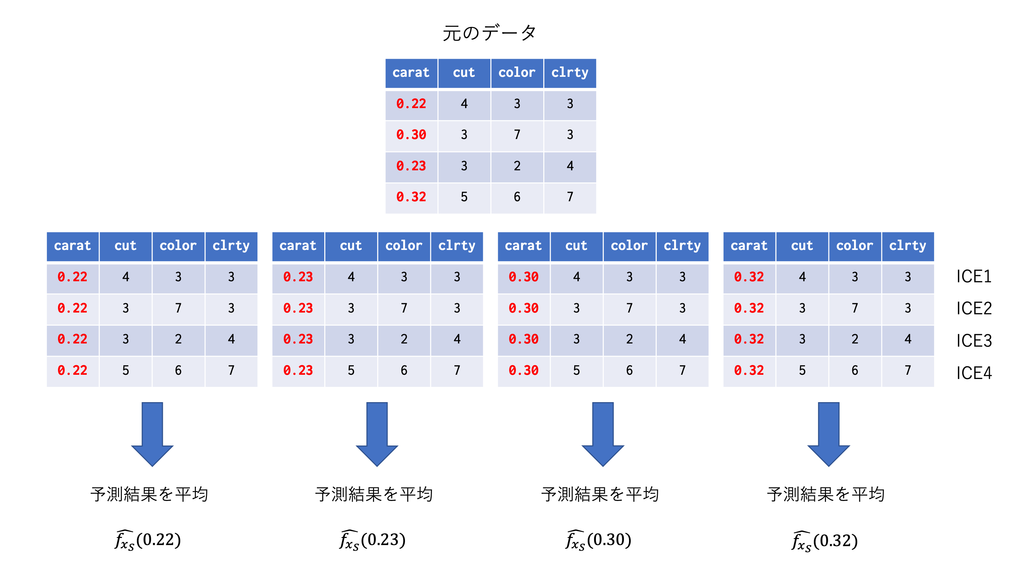
なお、PDPは平均をとりますが、平均を取らずに各について個別にプロットしたものをIndividual Conditional Expectation (ICE) Plotと呼びます。 特に変数間の交互作用がある場合にPDPでは見失ってしまう関係を確認することができます。

それでは、特に重要だった変数caratについて実際にPDPを作成してみましょう。パッケージはpdpを使います。

ice_carat = fitted %>% 
  partial(pred.var = "carat",
          pred.fun = pred_wrapper,
          train = df_test_baked, 
          type = "regression")

ice_carat %>% 
  autoplot()

partial()でPD/ICE Plotの元となるデータを計算できます。細部にこだわらなければautoplot()で可視化するのが一番手っ取り早いです。 赤い線がPDP、黒い線がICEになります。caratがlog(price)に与える影響が徐々に逓減していく様子が見て取れます。 事前に関数形の仮定を置かずにインプットとアウトカムの非線形な関係を柔軟に捉えることができるのがRF+PDPの強力な点かと思います。

まとめ

• モデルの解釈性は意思決定に繋がるデータ分析として重要
• 変数重要度とPDPでアルゴリズムによらずブラックボックスモデルを解釈することができる

アルゴリズムによらずモデルを解釈する手法としては他にもALE、SHAP value、LIMEなどがあり、次回以降に紹介できればと思っています。

参考

• Interpretable Machine Learning
• https://course.fast.ai/ml
• Learn Machine Learning Explainability Tutorials | Kaggle
• Ideas on interpreting machine learning – O’Reilly
• Introducing PDPbox. PDPbox is a partial dependence plot… | by Jiangchun Li | Towards Data Science
• Variable Importance Plots • vip
• Partial Dependence Plots • pdp

*1:変数間の関係が相関関係なのか因果関係なのかという問題はありますが

tidymodelsによるtidyな機械学習（その1：データ分割と前処理から学習と性能評価まで）

目次

※この記事をベースにした2019年12月7日に行われたJapan.R 2019での発表資料は以下になります。 tidymodelsによるtidyな機械学習 - Speaker Deck

はじめに

本記事ではtidymodelsを用いたtidyな機械学習フローを紹介したいと思います。

tidyverseはデータハンドリングと可視化のためのメタパッケージでしたが、tidymodelsはtydyverseにフィットするやり方で統計モデリング/機械学習をするためのメタパッケージになります。

tidymodels配下のパッケージは量が多く使い所が限られているパッケージも多いため、一度に全ては紹介できません。 ですので、今回は典型的な

1. 訓練データとテストデータの分割
2. 特徴量エンジニアリング
3. モデルの学習
4. モデルの精度評価

という機械学習フローを想定し、各パッケージの機能と連携をコンパクトにまとめたいと思います。

各パッケージの用途は以下になります。

• rsample：訓練データ/テストデータの分割
• recipe：特徴量エンジニアリング
• parsnip：異なるパッケージのアルゴリズムを同じシンタックスで扱えるようにするラッパー
• yardstic：モデルの精度評価

tidyな機械学習フロー

tidyverseとtidymodelsを読み込みます。

library(tidyverse)
library(tidymodels)

訓練データとテストデータの分割

まず第一に大元のデータを訓練データとテストデータに分割しましょう。

データはdiamondsを使って、ダイヤの価格を予測することにします。

set.seed(42)

df_split = initial_split(diamonds,  p = 0.8)

df_train = training(df_split)
df_test  = testing(df_split)

データ分割の役割はrsampleが担っています。

initial_split()で分割するデータと、訓練データが占める割合を指定します。

training()で訓練データを、testing()でテストデータを抽出できます。

特徴量エンジニアリング

次に特徴量エンジニアリングのためのレシピを作成します。作成したレシピを実際にデータに適用することで、処理済みのデータが作成されます。

どのような特徴量エンジニアリングが必要かは機械学習モデルに依存しますが、今回はRandom Forestを用いるための最低限の前処理を行います。

rec = recipe(price ~ carat + color + cut + clarity + depth, data = df_train) %>% 
  step_log(price) %>% 
  step_ordinalscore(all_nominal())

> rec
Data Recipe

Inputs:

      role #variables
   outcome          1
 predictor          9

Operations:

Log transformation on price
Scoring for all_nominal()

特徴量エンジニアリングのための関数はrecipeにまとめられています。

まずはrecipe()で用いる特徴量とデータを指定し、そこに処理をパイプで重ねていきます。

関数は全てstep_*()で統一されていて、今回用いたstep_log()は指定した変数の対数をとる関数で、step_ordinalscore()は順序のあるカテゴリカル変数を順序（1, 2, 3..）に変換します。 （tree系のモデルではなく線形モデルを用いる場合はstep_dummy()でダミー変数にできます。 *1

all_nominal()は全てのカテゴリカル変数を指定しています。他にもたとえばall_numeric()は全ての連続変数を指定できますし、starts_with()などのtidyverseではお馴染みの関数で指定することもできます。詳細は?selectionsをご確認下さい。

レシピができたので実際にデータに適用しましょう。

rec_preped = rec %>% 
  prep(df_train)

df_train_baked = rec_preped %>% 
  juice() 

> df_train_baked
# A tibble: 43,153 x 10
   carat   cut color clarity depth table     x     y     z price
   <dbl> <dbl> <dbl>   <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
 1 0.23      5     2       2  61.5    55  3.95  3.98  2.43  5.79
 2 0.21      4     2       3  59.8    61  3.89  3.84  2.31  5.79
 3 0.23      2     2       5  56.9    65  4.05  4.07  2.31  5.79
 4 0.290     4     6       4  62.4    58  4.2   4.23  2.63  5.81
 5 0.31      2     7       2  63.3    58  4.34  4.35  2.75  5.81
 6 0.24      3     7       6  62.8    57  3.94  3.96  2.48  5.82
 7 0.24      3     6       7  62.3    57  3.95  3.98  2.47  5.82
 8 0.26      3     5       3  61.9    55  4.07  4.11  2.53  5.82
 9 0.22      1     2       4  65.1    61  3.87  3.78  2.49  5.82
10 0.23      3     5       5  59.4    61  4     4.05  2.39  5.82
# ... with 43,143 more rows

prep()に訓練データを指定し、訓練データの変換を行います。

さらにjuice()で変換されたデータを抽出することができます。

priceに対数がとられてカテゴリカル変数が（cut, color, clarity）が順序になっているのがわかるかと思います。

次に同じレシピを用いてテストデータも変換します。

df_test_beked = rec_preped %>% 
  bake(df_test)

> df_test_baked
# A tibble: 10,787 x 10
   carat   cut color clarity depth table price     x     y     z
   <dbl> <dbl> <dbl>   <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
 1  0.22     4     3       3  60.4    61  5.83  3.88  3.84  2.33
 2  0.3      3     7       3  62.7    59  5.86  4.21  4.27  2.66
 3  0.23     3     2       4  63.8    55  5.86  3.85  3.92  2.48
 4  0.23     3     1       4  60.5    61  5.88  3.96  3.97  2.4 
 5  0.23     3     2       5  59.5    58  6.00  4.01  4.06  2.4 
 6  0.23     2     3       5  58.2    59  6.00  4.06  4.08  2.37
 7  0.33     5     6       2  61.8    55  6.00  4.49  4.51  2.78
 8  0.33     5     7       3  61.1    56  6.00  4.49  4.55  2.76
 9  0.3      3     6       3  62.6    57  6.00  4.25  4.28  2.67
10  0.3      4     1       3  62.6    59  6.31  4.23  4.27  2.66
# ... with 10,777 more rows

レシピを新しいデータに適用する場合はbake()を使います*2。

モデルの学習

recipeで訓練データ/テストデータをモデルに投入できる形に変換できたので、次はparsnipで学習モデルを定義しましょう。

Rで機械学習を行う際、学習アルゴリズムごとにパッケージが分かれていて、それ故シンタックスが統一されておらず、各々のシンタックスを覚えるのが大変でした（たとえば入力はformulaなのかmatrixなのかなど）。

これを統一的なシンタックスで扱えるようにするメタパッケージとして、たとえばcaretがありましたが、最近よりtidyverseに馴染むパッケージとしてparsnipが開発されました*3。 ちなみに開発者はcaretと同じくMax Kuhnです。

rf = rand_forest(mode = "regression", 
                 trees = 50,
                 min_n = 10,
                 mtry = 3) %>% 
  set_engine("ranger", num.threads = parallel::detectCores(), seed = 42)

> rf
Random Forest Model Specification (regression)

Main Arguments:
  mtry = 3
  trees = 50
  min_n = 10

Engine-Specific Arguments:
  num.threads = parallel::detectCores()
  seed = 42

Computational engine: ranger 

rand_forest()は学習アルゴリズムとしてRandom Forestを使用します。今回は回帰問題なのでmode=regressionとしています。 rand_forest()で指定できるハイパーパラメータは3つあり、それぞれ

• trees：作成する決定木の数。
• min_n：ノードに最低限含まれるサンプル数。
• mtry：各ノードで分割に用いる特徴量の数。

となります。今回は適当に指定しました。

さらにset_engine()でRandom Forestに用いるパッケージを指定でき、ここではranger を指定しています。 set_engine()内でranger固有のパラメータを指定でき、コア数とシードを指定しました。

モデルが定義できたので、学習を行います。これはfit()にモデル式と入力データを指定するだけで完結します。

fitted = rf %>% 
  fit(price ~ ., data = df_train_baked)

> fitted
parsnip model object

Ranger result

Call:
 ranger::ranger(formula = formula, data = data, mtry = ~3, num.trees = ~50,      min.node.size = ~10, num.threads = ~parallel::detectCores(),      seed = ~42, verbose = FALSE) 

Type:                             Regression 
Number of trees:                  50 
Sample size:                      43153 
Number of independent variables:  9 
Mtry:                             3 
Target node size:                 10 
Variable importance mode:         none 
Splitrule:                        variance 
OOB prediction error (MSE):       0.009112244 
R squared (OOB):                  0.9911622 

モデルの精度評価

学習が済んだので、最後に予測精度を評価しましょう。 テストデータへの予測はpredict() で行います。

df_result = df_test_baked %>% 
  select(price) %>% 
  bind_cols(predict(fitted, df_test_baked))
  
> df_result
# A tibble: 10,787 x 2
   price .pred
   <dbl> <dbl>
 1  5.83  5.95
 2  5.86  5.98
 3  5.86  5.97
 4  5.88  5.97
 5  6.00  6.00
 6  6.00  5.99
 7  6.00  6.14
 8  6.00  6.14
 9  6.00  6.03
10  6.31  6.33
# ... with 10,777 more rows

予測結果に対してyardsticの評価指標関数を適用することでモデルの性能が評価できます。 yardsticには様々な評価指標関数が含まれており、個別で指定することもできますが、matrics()は回帰モデルの結果に対してRMSE、MAE、R²をまとめて計算してくれます。

> df_result %>% 
+   metrics(price, .pred)
# A tibble: 3 x 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 rmse    standard      0.0910
2 rsq     standard      0.992 
3 mae     standard      0.0671

まとめ

本記事ではtidymodelsによる

1. rsampleで訓練データ/テストデータの分割し、
2. recipeで特徴量エンジニアリングを行い、
3. parsnipでモデルを定義・学習し、
4. yardsticで性能を評価

する、tidyな機械学習フローを紹介しました。

各パッケージにはまだまだ多くの機能があり、今回紹介できたのは最低限の機能のみです。

次回はtidymodelsで交差検証を行い、ハイパーパラメータをチューニングする方法をご紹介できればと思っています。

参考文献

• tidymodels
  • tidymodels · GitHub
• rsample
  • General Resampling Infrastructure • rsample
• recipe
  • Preprocessing Tools to Create Design Matrices • recipes
  • Rパッケージ recipes の紹介 「うまい飯を作る」
  • モデルで扱うデータの前処理をrecipesで行う - 株式会社ホクソエムのブログ
• parsnip
  • A Common API to Modeling and Analysis Functions • parsnip
• yardstic
  • Tidy Characterizations of Model Performance • yardstick

*1: recipeの他のstep関数やselectorは以下をご確認下さい。Function reference • recipes

*2:今回tree系のモデルなので標準化はやっていませんが、たとえば標準化を行う場合は訓練データの平均と分散を用いてテストデータの標準化が行われます。

*3:parsnipが対応しているパッケージは以下を御覧ください：List of Models • parsnip

Ridge回帰の使い所を考える

はじめに

本記事では回帰係数の推定方法としてのRidge回帰（L2正則化）の使い所について考えたいと思います。
結論から言うと、サンプルサイズが不十分な状況下でRidge回帰を用いてより真の値に近い回帰係数を得る確率を高めるという使い方ができそうです。

OLS推定量とRidge推定量

簡単のために、以下の線形回帰モデルを考えます。

\begin{align}
Y = X\beta + \epsilon
\end{align}

ここで、は の行列で、はの列ベクトルとします。 はサンプルサイズ、 は特徴量の数になります。
このとき、OLS推定量は二乗誤差を最小にするようなで与えられます。
\begin{align}
\widehat{\beta}_{\mathrm{OLS}} &= \arg\min_b \left(Y - X b\right)^\top\left(Y - X b\right) \\
&= \left(X^\top X \right)^{-1}X^\top Y
\end{align}

標準的な仮定のもとで、OLS推定量は推定量 は真の値の一致推定量となることが知られています。*1

これに対して、 のとれる値に制限をかけることで過学習を抑えようとするのがRidge回帰になります。
具体的にはOLSの目的関数に正則化項を付け加えたものを最小化します。は正則化の強さを表すハイパーパラメータになります。

\begin{align}
\widehat{\beta}_{\mathrm{Ridge}} &= \arg\min_b \left(Y - X b\right)^\top\left(Y - X b\right) + \lambda||b||^2 \\
&= \left(X^\top X + \lambda I_K \right)^{-1}X^\top Y
\end{align}

ここではの単位行列です。
と を比較すれば明らかですが、両者の違いはのみです。
なので、のときOLS推定量とRidge推定量は完全に一致します。反対にを大きくするとRidge推定量は0方向に引っ張られます。
つまり、Ridge回帰はパラメータが極端な値を取らないよう安定させる（過学習を抑える）というリターンを得るために、（多少の）バイアスがかかるという犠牲を払うモデルであると言えます。
これは機械学習の文脈でバイアスとバリアンスのトレードオフとしてよく知られています。

シミュレーション

それでは実際にOLSとRidge回帰の挙動の違いについてシミュレーションで確認してみましょう。
まずは必要なパッケージを読み込みます。*2

import pandas as pd
import numpy as np

from sklearn.linear_model import LinearRegression, Ridge,  RidgeCV
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_spd_matrix #分散共分散行列を作る

from plotnine import * # 可視化用。

ちょっと極端な方が結果がクリアに見えると思うので、サンプルサイズは100しかないんだけど80個の特徴量について回帰係数を推定したい、というシチュエーションを想定することにします。
下記のコードではランダムにデータを生成してOLSとRidge回帰で回帰係数を推定する、ということを繰り返しています。

np.random.seed(42)
I = 1000
N = 100
K = 80

beta = np.random.uniform(-1, 1, K)

betas = np.zeros((I, 2, K))
for i in range(I):
    X = np.random.multivariate_normal(np.zeros(K), make_spd_matrix(K), N)
    X = StandardScaler().fit_transform(X)
    U = np.random.normal(0, 1, N)
    Y = X @ beta + U
    
    if i == 0: #一回目のループでRidgeのハイパーパラメータを決める
        ridge_alpha = RidgeCV(alphas=np.random.uniform(0.1, 20, 100), cv=5).fit(X, Y).alpha_
        print(f'ridge: {ridge_alpha}')
    
    beta_ols = LinearRegression().fit(X, Y).coef_
    
    beta_ridge = Ridge(alpha=ridge_alpha).fit(X, Y).coef_
    
    betas[i, :, :] = np.concatenate([beta_ols[:, np.newaxis], beta_ridge[:, np.newaxis]], axis=1).T
    
    if i % 200 == 0:
        print(i)

# 可視化のためにシミュレーションの結果をデータフレームとして持ち直す
df = None
for i in range(I):
    tmp = (pd.DataFrame(data = betas[i, :, :].T, columns=['OLS', 'Ridge'])
           .assign(Truth = beta, k = lambda df: df.index, i = i))
    
    if df is None:
        df = tmp
    else:
        df = df.append(tmp)
        
df = df.melt(id_vars=['i', 'k', 'Truth'], value_vars=['OLS', 'Ridge'], value_name='coefficient', var_name='method')

シミュレーションの結果を可視化してみましょう。

g = (ggplot(aes('factor(k)', 'coefficient', fill='method', color='method'), df[df.k.between(1, 10)]) +
     geom_hline(yintercept=0, size=1, color='gray') +
     geom_violin(alpha=0.5) +
     geom_point(aes('factor(k)', 'Truth'), size=4, color='black', fill='black') +
     scale_fill_brewer(name='Method', type='qual',palette='Dark2') +
     scale_color_brewer(name = 'Method', type='qual',palette='Dark2') + 
     lims(y=(-3, 3)) + 
     labs(x='beta_hat(k)', y='Coefficient') + 
     theme_bw() +
     theme(figure_size=(15, 7)))

print(g)

図は初めの10個の回帰係数を取り出して、シミュレーション1000回分の回帰係数の分布を確認しています。
縦軸が回帰係数の値、横軸が回帰係数の番号です。
真ん中の黒い点が真の回帰係数の値で、緑がOLSで求めた回帰係数の分布、オレンジがRidge回帰での分布になります。

図からは各手法で求めた回帰係数について、以下の性質が見て取れます。

• OLSの場合はバイアスがなく真の値を中心に分布しているが、その分散は大きく、見当はずれの値を取ることもある
• Ridge回帰の場合はゼロ方向にバイアスがかかっている。その一方で回帰係数は非常に安定しており、真の値に近い部分に密度高く分布しており、極端な値を取ることもない。

Ridge回帰の使いどころ

数式とシミュレーションの結果から、サンプルサイズが不十分な状況下でRidge回帰を用いてより真の値に近い回帰係数を得る確率を高めるという使い方が考えられそうです。*3
特に、特徴量のインパクトを見える際により保守的な推定をしたい場合には有効と言えそうです。Ridge回帰は極端な回帰係数をとらず、またRidge回帰のバイアスは0方向にかかるので、Ridge回帰ではより控え目なインパクトが推定されると言えるかと思います。

*1:https://www.ssc.wisc.edu/~bhansen/econometrics/

*2:ちなみにplotnineはRの代表的な可視化パッケージであるggplot2と同じ記法が使えるpython用のパッケージです。若干制限もありますが、ggplot2に慣れたRユーザーにとっては使いやすいかと思います。

*3:サンプルサイズが十分な状況ではOLSで一致推定を行うのが妥当かと思います。